Advertisements
Advertisements
प्रश्न
In the following figure, if LM || CB and LN || CD, prove that `("AM")/("AB")=("AN")/("AD")`

उत्तर
In ΔABC, LM || CB ...[given]
∴ Using the basic proportionality theorem, we have
`("AM")/("MB") = ("AL")/("LC")`
⇒ `("MB")/("AM") = ("LC")/("AL")`
⇒ `("MB")/("AM") + 1=("LC")/("AL") + 1` ...[adding 1 on both sides]
⇒ `("MB" + "AM")/("AM") = ("LC" + "AL")/("AL")`
⇒ `("AB")/("AM") = ("AC")/("AL")`
⇒ `("AM")/("AB") = ("AL")/("AC")` ...(1)
Similarly in ΔACD, LN || CD, we have
`("AL")/("AC") = ("AN")/("AD")` ...(2)
From (1) and (2)
`("AM")/("AB") = ("AL")/("AC") = ("AN")/("AD")`
⇒ `("AM")/("AB") = ("AN")/("AD")` ...(Proved)
APPEARS IN
संबंधित प्रश्न
In figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm, AP = 2.8 cm, find CA and AQ.
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
In the adjoining figure, ABC is a right angled triangle with ∠BAC = 90°.
1) Prove ΔADB ~ ΔCDA.
2) If BD = 18 cm CD = 8 cm Find AD.
3) Find the ratio of the area of ΔADB is to an area of ΔCDA.

State, true or false:
All isosceles triangles are similar.
In the given figure, ∆ABC and ∆AMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
- Prove that: ∆ABC ~ ∆AMP
- Find: AB and BC.

E and F are the points in sides DC and AB respectively of parallelogram ABCD. If diagonal AC
and segment EF intersect at G; prove that:
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that: `(FB)/(AD) = (BC)/(ED)`.

In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.

In the given figure, DB⊥BC, DE⊥AB and AC⊥BC.
Prove that `(BE)/(DE)=(AC)/(BC)`

A vertical pole of length 7.5 cm casts a shadow 5 m long on the ground and at the same time a tower casts a shadow 24 m long. Find the height of the tower.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(ΔADE) = `15cm^2`, find the area of ΔABC.

In the given figure, ∠ABC = 75°, ∠EDC = 75° state which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.


O is any point in the interior of ΔABC. Bisectors of ∠AOB, ∠BOC and ∠AOC intersect side AB, side BC, side AC in
F, D and E respectively.
Prove that
BF × AE × CD = AF × CE × BD
In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`

In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
ABCD and PQRS are similar figures. AB= 12cm, BC=x cm, CD= 15 cm, AD= 10 cm, PQ= 8 cm, QR = 5 cm, RS = m cm and PS = n cm .Find the values of x, m and n.
D and E are points on the sides AB and AC respectively of Δ ABC such that AB=5.6cm, AD= 1.4cm, AC=7 .2cm and AE = 1.5 cm, show that DE is parallel to BC
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find
The area on the map that represents the plot of land.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if:
- AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.
- AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
In the figure, given below, PQR is a right-angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

In fig.DE || BC ,AD = 1 cm and BD = 2 cm. what is the ratio of the ar(ΔABC) to the ar (ΔADE)?

Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are `3/5` of the corresponding sides of ΔABC.
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are `3/5` of the corresponding sides of the first triangle.
Points A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b.
Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"AC"`
ABCD is a parallelogram whose sides AB and BC are 18cm and 12cm respectively. G is a point on AC such that CG : GA = 3 : 5 BG is produced to meet CD at Q and AD produced at P. Prove that ΔCGB ∼ ΔAGP. Hence, fi AP.
In the given figure, PB is the bisector of ABC and ABC =ACB. Prove that:
a. BC x AP = PC x AB
b. AB:AC = BP: BC
In a right-angled triangle ABC, ∠B = 90°, P and Q are the points on the sides AB and AC such as PQBC, AB = 8 cm, AQ = 6 cm and PA:AB = 1:3. Find the lengths of AC and BC.
Given that ΔABC ∼ ΔPRQ, name the corresponding angles and the corresponding sides.
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
ΔXYZ is enlarged to ΔX'Y'Z'. If XY = 12cm, YZ = 8cm and XZ = 14cm and the smallest side of ΔX'Y'Z' is 12cm, find the scale factor and use it to find the length of the other sides of the image ΔX'Y'Z'.
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The ground area in km2 that is represented by 2cm2 on the map.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The volume of the model if the volume of the truck is 6m3
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
Check whether the triangles are similar and find the value of x
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is
Two similar triangles will always have ________ angles
If in triangles PQR and XYZ, `"PQ"/"XY" = "QR"/"ZX"` then they will be similar if
ΔABC ~ ΔDEF. Write the ratios of their corresponding sides
In the figure PQ || BC. If `"PQ"/"BC" = 2/5` then `"AP"/"PB"` is ______.

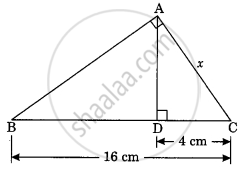
In the given figure the value of x is
In a square of side 10 cm, its diagonal = ______.
In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that `(AE)/(ED) = (BF)/(FC)`.

In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

