Advertisements
Advertisements
प्रश्न
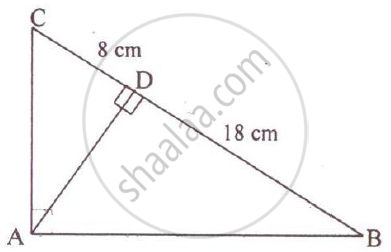
In the adjoining figure, ABC is a right angled triangle with ∠BAC = 90°.
1) Prove ΔADB ~ ΔCDA.
2) If BD = 18 cm CD = 8 cm Find AD.
3) Find the ratio of the area of ΔADB is to an area of ΔCDA.

उत्तर
1) Let ∠CAD = x
⇒ ∠DAB = 90° - x
∠DAB = 180 - (90° + 90° - x) = x
∠CAD =- ∠DBA .....(1)
In ΔADB and ΔCDA
∠ADB = ∠ADC [each 90°]
∠ABD = ∠CAD [From 1]
∴ ΔADB ~ ΔCDA (AA similarity criterion)
2) Since the corresponding sides of similar triangles are proportional.
`:. (CD)/(AD) = (DA)/(DB)`
`=> AD^2 = DB xx CD`
`=> AD^2 = 18 xx 8`
`=> AD = 12 cm`
3) The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
So `(Ar(ΔADB))/(Ar(ΔCDA)) = ("AD"^2)/"CD"^2 = 144/64 = 9/4`
Thus, the required ratio is 9: 4.
APPEARS IN
संबंधित प्रश्न
The perimeters of two similar triangles ABC and PQR are respectively 36 cm and 24 cm. If PQ = 10 cm, find AB
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
In ΔPQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP.
Prove that : (i) ΔPQL ∼ ΔRPM
(ii) QL. Rm = PL. PM
(iii) PQ2 = QR. QL.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The volume of the model if the volume of the truck is 6m3
A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in the same line, find the height of the lamp post.
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
Areas of two similar triangles are equal then prove that triangles are congruent
In the given figure, ∠ACB = ∠CDA, AC = 8cm, AD = 3cm, then BD is ______.

