Advertisements
Advertisements
प्रश्न
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio.
उत्तर
Given: Let a ΔABC in which a line DE parallel to BC intersects AB at D and AC at E.
To Prove: DE divides the two sides in the same ratio.
`"AD"/"DB" = "AE"/"EC"`
Construction: Join BE, CD and draw EF ⊥ AB and DG ⊥ AC.
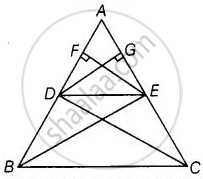
Proof: Here,
Area of triangle = `1/2` × base × height
Area of ΔADE = `1/2` × AD × EF
or
Area of ΔADE = `1/2` × AE × DG
Similarly,
Area of ΔBDE = `1/2` × DB × EF
Area of ΔDEC = `1/2` × EC × DG
`"ar(ΔADE)"/"ar(ΔBDE)" = (1/2 × "AD" × "EF")/(1/2 × "DB" × "EF")`
`"ar(ΔADE)"/"ar(ΔBDE)" = "AD"/"DB"` ...(1)
From (2) and (4),
`"ar(ΔADE)"/"ar(ΔDEC)" = (1/2 × "AE" × "DG")/(1/2 × "EC" × "DG")`
`"ar(ΔADE)"/"ar(ΔDEC)" = "AE"/"EC"` ...(2)
Since, ΔBDE and ΔDEC lie between the same parallel DE and BC and on the same base DE.
∴ ar(ΔBDE) = ar(ΔDEC) ...(3)
From (1), (2) and (3), we get,
`"AD"/"BD" ="AE"/"EC"`
Hence proved.
APPEARS IN
संबंधित प्रश्न
In figure, ABCD is a trapezium with AB || DC. If ∆AED is similar to ∆BEC, prove that AD = BC.
In the following figure, if LM || CB and LN || CD, prove that `("AM")/("AB")=("AN")/("AD")`

In the following figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

In the given figure, AB and DE are perpendicular to BC.

1) Prove that ΔABC ∼ ΔDEC
2) If AB = 6 cm; DE = 4 cm and AC = 15 cm. Calculate CD.
3) Find the ratio of area of ΔABC: area of ΔDEC
State, true or false:
All isosceles triangles are similar.
ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
In the given figure, DE║BC and DE: BC = 3:5. Calculate the ratio of the areas of ΔADE and the trapezium BCED.

State the AA-similarity criterion
In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.

In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.
In Δ ABC , MN || BC .

If `"AB"/"AM" = 9/4` , find `("Ar" ("trapezium MBCN"))/("Ar" . (triangle "ABC"))`
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in cm, of the model; if the length of the aeroplane is 40 m.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
The dimensions of the model of a multistorey building are 1.2 m × 75 cm × 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.

In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2 PD

Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are `3/5` of the corresponding sides of ΔABC.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AD = 5.7cm, BD = 9.5cm, AE = 3.3cm, and EC = 5.5cm
If ΔPQR, AB is drawn parallel to QR. If PQ = 9cm, PR = 6cm and PB = 4.cm, find the length of AP.
The sides PQ and PR of the ΔPQR are produced to S and T respectively. ST is drawn parallel to QR and PQ: PS = 3:4. If PT = 9.6 cm, find PR. If 'p' be the length of the perpendicular from P to QR, find the length of the perpendicular from P to ST in terms of 'p'.
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
ΔABC is enlarged, with a scale factor 5. Find: A'B', if AB = 4cm
ΔPQR ~ ΔSUV. Write pairs of congruent angles
ΔDEF ~ ΔABC. If DE : AB = 2 : 3 and ar ΔDEF is equal to 44 square units then ar (ΔABC) (square unit) is ______.
ΔABC and ΔBDE are two equilateral triangles such that D is the mid point of BC. Ratio of the areas of triangle ΔABC and ΔBDE is ______.
