English Medium
Academic Year: 2018-2019
Date: मार्च 2019
Duration: 3h
Advertisements
(i) All questions are compulsory.
(ii) The question paper consists of 30 questions divided into four sections – A, B, C and D.
(iii) Section A comprises 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8questions of 4 marks each.
(iv) There is no overall choice. However, an internal choice has been provided in two questions of 1mark, two questions of 2 marks, four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternative in all such questions.
(v) Use of calculators is not permitted.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
Chapter: [0.042] Circles

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
Chapter: [0.031] Lines (In Two-dimensions)
If tan α =`5/12` find the value of sec α.
Chapter: [0.024] Arithmetic Progressions
Write the discriminant of the quadratic equation (x + 5)2 = 2 (5x − 3).
Chapter: [0.023] Quadratic Equations
Find after how many places of decimal the decimal form of the number `27/(2^3. 5^4. 3^2)` will terminate.
Chapter: [0.011000000000000001] Real Numbers
Express 429 as a product of its prime factors.
Chapter: [0.011000000000000001] Real Numbers
Find the sum of the first 10 multiples of 6.
Chapter: [0.024] Arithmetic Progressions
Find the positive value of m for which the distance between the points A(5, −3) and B(13, m) is 10 units.
Chapter: [0.053] Some Applications of Trigonometry
A die is thrown once. Find the probability of getting a composite number
Chapter: [0.07200000000000001] Probability [0.07200000000000001] Probability
A die is thrown once. Find the probability of getting a prime number.
Chapter: [0.07200000000000001] Probability
Cards numbered 7 to 40 were put in a box. Poonam selects a card at random. What is the probability that Poonam selects a card which is a multiple of 7?
Chapter: [0.07200000000000001] Probability [0.07200000000000001] Probability
Points A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b.
Chapter: [0.040999999999999995] Triangles [0.040999999999999995] Triangles [0.040999999999999995] Triangles
Points P and Q trisect the line segment joining the points A(−2, 0) and B(0, 8) such that P is near to A. Find the coordinates of points P and Q.
Chapter: [0.033] Constructions
Solve the following pair of linear equations:
3x − 5y = 4
2y + 7 = 9x
Chapter: [0.022000000000000002] Pair of Linear Equations in Two Variables
If HCF of 65 and 117 is expressible in the form 65n − 117, then find the value of n.
Chapter: [0.011000000000000001] Real Numbers
Advertisements
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
Chapter: [0.053] Some Applications of Trigonometry
In the quadratic equation kx2 − 6x − 1 = 0, determine the values of k for which the equation does not have any real root.
Chapter: [0.023] Quadratic Equations
A, B and C are interior angles of a triangle ABC. Show that
sin `(("B"+"C")/2) = cos "A"/2`
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
A, B and C are interior angles of a triangle ABC. Show that
If ∠A = 90°, then find the value of tan`(("B+C")/2)`
Chapter: [0.051] Introduction to Trigonometry [0.052000000000000005] Trigonometric Identities
If tan (A + B) = 1 and tan(A-B)`=1/sqrt3` , 0° < A + B < 90°, A > B, then find the values of A and B.
Chapter: [0.051] Introduction to Trigonometry
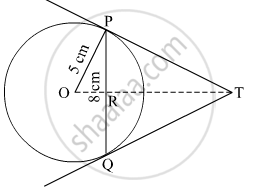
In Figure 2, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
Chapter: [0.033] Constructions
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Chapter: [0.042] Circles
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.
| Number of days: | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | 36-42 |
| Number of students: | 10 | 11 | 7 | 4 | 4 | 3 | 1 |
Chapter: [0.071] Statistics
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
Chapter: [0.061] Areas Related to Circles
The perpendicular from A on side BC of a Δ ABC meets BC at D such that DB = 3CD. Prove that 2AB2 = 2AC2 + BC2.
Chapter: [0.040999999999999995] Triangles
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
Chapter: [0.040999999999999995] Triangles
Check whether g(x) is a factor of p(x) by dividing polynomial p(x) by polynomial g(x),
where p(x) = x5 − 4x3 + x2 + 3x +1, g(x) = x3 − 3x + 1
Chapter: [0.021] Polynomials
Prove that `sqrt3` is an irrational number.
Chapter: [0.011000000000000001] Real Numbers
Advertisements
Find the largest number which on dividing 1251, 9377 and 15628 leave remainders 1, 2 and 3 respectively.
Chapter: [0.011000000000000001] Real Numbers
Find the area of the triangle ABC with the coordinates of A as (1, −4) and the coordinates of the mid-points of sides AB and AC respectively are (2, −1) and (0, −1).
Chapter: [0.040999999999999995] Triangles [0.040999999999999995] Triangles [0.040999999999999995] Triangles
Two numbers are in the ratio of 5: 6. If 7 is subtracted from each of the numbers, the ratio becomes 4: 5. Find the numbers.
Chapter: [0.011000000000000001] Real Numbers
Water is flowing at the rate of 2.52 km/h through a cylindrical pipe into a cylindrical tank, the radius of whose base is 40 cm. If the increase in the level of water in the tank, in half an hour is 3.15 m, find the internal diameter of the pipe.
Chapter: [0.062] Surface Areas and Volumes

In Figure 3, a decorative block is shown which is made of two solids, a cube, and a hemisphere. The base of the block is a cube with an edge 6 cm and the hemisphere fixed on the top has a diameter of 4⋅2 cm. Find
(a) the total surface area of the block.
(b) the volume of the block formed. `("Take" pi = 22/7)`
Chapter: [0.062] Surface Areas and Volumes
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
Chapter: [0.053] Some Applications of Trigonometry
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Chapter: [0.040999999999999995] Triangles [0.040999999999999995] Triangles [0.040999999999999995] Triangles
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Chapter: [0.040999999999999995] Triangles
Change the following distribution to a 'more than type' distribution. Hence draw the 'more than type' ogive for this distribution.
| Class interval: | 20−30 | 30−40 | 40−50 | 50−60 | 60−70 | 70−80 | 80−90 |
| Frequency: | 10 | 8 | 12 | 24 | 6 | 25 | 15 |
Chapter: [0.071] Statistics
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was 60°. Find the height of the tower.
Chapter: [0.053] Some Applications of Trigonometry
If m times the mth term of an Arithmetic Progression is equal to n times its nth term and m ≠ n, show that the (m + n)th term of the A.P. is zero.
Chapter: [0.024] Arithmetic Progressions
The sum of the first three numbers in an Arithmetic Progression is 18. If the product of the first and the third term is 5 times the common difference, find the three numbers.
Chapter: [0.024] Arithmetic Progressions
A shopkeeper buys some books for Rs 80. If he had bought 4 more books for the same amount, each book would have cost Rs 1 less. Find the number of books he bought.
Chapter: [0.011000000000000001] Real Numbers
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
Chapter: [0.042] Circles
Prove the following:
`1/(1+sin^2theta) + 1/(1+cos^2theta) + 1/(1+sec^2theta) + 1/(1+cosec^2theta) = 2`
Chapter: [0.051] Introduction to Trigonometry [0.051] Introduction to Trigonometry
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2018 - 2019
Previous year Question paper for CBSE Class 10 Maths-2019 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
