Question

Points P and Q trisect the line segment joining the points A(−2, 0) and B(0, 8) such that P is near to A. Find the coordinates of points P and Q.

Answer 1

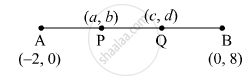
P and Q trisect line joining the points A and B. 
Let the coordinates of P and Q be (a, b) and (c, d) respectively. 
P is the midpoint of AQ.

${\displaystyle \frac{-2+\text{c}}{2}=\text{a}\text{and}\frac{0+\text{d}}{2}=\text{b}}$

⇒ c= 2a + 2 and d = 2b   ...........(1)

Also, Q is the mid point of PB.

${\displaystyle \frac{\text{a}+0}{2}=\text{c}\text{and}\frac{\text{b}+8}{2}=\text{d}}$

⇒ ${\displaystyle \frac{\text{a}}{2}=\text{c}\text{and}\frac{\text{b}+8}{2}=\text{d}}$   .........(2)

From (1) and (2) we have

2a + 2 =${\displaystyle \frac{\text{a}}{2}}$

⇒ 4a + 4 = a

⇒ 3a = -4

⇒${\displaystyle \text{a}=-\frac{4}{3}}$

Also,

2b ${\displaystyle =\frac{\text{b}+8}{2}}$

⇒ 4b = b +8

⇒ b = ${\displaystyle \frac{8}{3}}$

Putting these values of a and b in (2)

${\displaystyle \frac{\frac{-4}{3}}{2}=\text{c}}$

⇒ ${\displaystyle \frac{-2}{3}=\text{c}}$

And 

${\displaystyle \frac{\frac{8}{3}+8}{2}=\text{d}}$

${\displaystyle \frac{\frac{8+24}{3}}{2}=\text{d}}$

⇒${\displaystyle \frac{\frac{32}{2}}{2}=\text{d}}$

⇒ ${\displaystyle \frac{16}{3}=\text{d}}$

Thus, the points are P ${\displaystyle (\frac{-4}{3},\frac{8}{3})}$ and Q ${\displaystyle (\frac{-2}{3},\frac{16}{3}).}$