Advertisements
Advertisements
Question
Points P and Q trisect the line segment joining the points A(−2, 0) and B(0, 8) such that P is near to A. Find the coordinates of points P and Q.
Solution
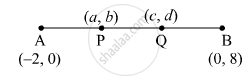
P and Q trisect line joining the points A and B.
Let the coordinates of P and Q be (a, b) and (c, d) respectively.
P is the midpoint of AQ.
`(-2 +"c")/2 = "a" and (0+"d")/2 = "b"`
⇒ c= 2a + 2 and d = 2b ...........(1)
Also, Q is the mid point of PB.
`("a"+0)/2 ="c" and ("b"+8)/2 = "d"`
⇒ `"a"/2 = "c" and ("b"+8)/2 ="d"` .........(2)
From (1) and (2) we have
2a + 2 =`"a"/2`
⇒ 4a + 4 = a
⇒ 3a = -4
⇒`"a" = -4/3`
Also,
2b `=("b"+8)/2`
⇒ 4b = b +8
⇒ b = `8/3`
Putting these values of a and b in (2)
`((-4)/3)/2 = "c"`
⇒ `(-2)/3 = "c"`
And
`(8/3+8)/2 = "d"`
`((8+24)/3)/2 = "d"`
⇒`(32/2)/2 = "d"`
⇒ `16/3 = "d"`
Thus, the points are P `((-4)/3 , 8/3)` and Q `((-2)/3 , 16/3).`
APPEARS IN
RELATED QUESTIONS
Write down the equation of a line whose slope is 3/2 and which passes through point P, where P divides the line segment AB joining A(-2, 6) and B(3, -4) in the ratio 2 : 3.
Construct the circumcircle and incircle of an equilateral triangle ABC with side 6 cm and centre O. Find the ratio of radii of circumcircle and incircle.
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are`4/5` times the corresponding sides of ΔABC.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose side are `1 1/2` times the corresponding sides of the isosceles triangle.
Give the justification of the construction
Construct a triangle similar to a given ΔABC such that each of its sides is (5/7)th of the corresponding sides of Δ ABC. It is given that AB = 5 cm, BC = 7 cm and ∠ABC = 50°.
∆AMT ~ ∆AHE. In ∆AMT, AM = 6.3 cm, ∠TAM = 50°, AT = 5.6 cm. `"AM"/"AH" = 7/5`. Construct ∆AHE.
Δ SHR ∼ Δ SVU. In Δ SHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and
SHSV = 53 then draw Δ SVU.
Find the ratio in which the segment joining the points (1, –3) and (4, 5) is divided by the x-axis? Also, find the coordinates of this point on the x-axis.
When a line segment is divided in the ratio 2 : 3, how many parts is it divided into?
If you need to construct a triangle with point P as one of its vertices, which is the angle that you need to construct a side of the triangle?