Advertisements
Advertisements
Question
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose side are `1 1/2` times the corresponding sides of the isosceles triangle.
Give the justification of the construction
Solution
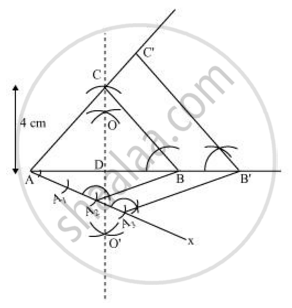
Let us assume that ΔABC is an isosceles triangle having CA and CB of equal lengths, base AB of 8 cm, and AD is the altitude of 4 cm.
A ΔAB'C' whose sides are 3/2 times of ΔABC can be drawn as follows.
Step 1
Draw a line segment AB of 8 cm. Draw arcs of same radius on both sides of the line segment while taking point A and B as its centre. Let these arcs intersect each other at O and O'. Join OO'. Let OO' intersect AB at D.
Step 2
Taking D as centre, draw an arc of 4 cm radius which cuts the extended line segment OO' at point C. An isosceles ΔABC is formed, having CD (altitude) as 4 cm and AB (base) as 8 cm.
Step 3
Draw a ray AX making an acute angle with line segment AB on the opposite side of vertex C.
Step 4
Locate 3 points (as 3 is greater between 3 and 2) A1, A2, and A3 on AX such that AA1 = A1A2 = A2A3.
Step 5
Join BA2 and draw a line through A3 parallel to BA2 to intersect extended line segment AB at point B'.
Step 6
Draw a line through B' parallel to BC intersecting the extended line segment AC at C'. ΔAB'C' is the required triangle.
Justification
The construction can be justified by proving that
`AB' = 3/2 AB, B'C' = 3/2 BC, AC' = 3/2 AC`
In ΔABC and ΔAB'C',
∠ABC = ∠AB'C' (Corresponding angles)
∠BAC = ∠B'AC' (Common)
∴ ΔABC ∼ ΔAB'C' (AA similarity criterion)
`=> (AB)/(AB')= (BC)/(B'C') = (AC)/(AC') ....(1)`
In ΔAA2B and ΔAA3B',
∠A2AB = ∠A3AB' (Common)
∠AA2B = ∠AA3B' (Corresponding angles)
∴ ΔAA2B ∼ ΔAA3B' (AA similarity criterion)
`=> (AB)/(AB') = (`
`=>(AB)/(AB') = 2/3 .....2`
On comparing equations (1) and (2), we obtain
`(AB)/(AB')=(BC)/(B'C') = (AC)/(AC') = 2/3`
`=> AB' = 3/2 AB, B'C' = 3/2 BC, AC' = 3/2 AC`
This justifies the construction.
APPEARS IN
RELATED QUESTIONS
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are`4/5` times the corresponding sides of ΔABC.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are `4/3 `times the corresponding side of ΔABC. Give the justification of the construction.
Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
Find the ratio in which point T(–1, 6)divides the line segment joining the points P(–3, 10) and Q(6, –8).
ΔABC ~ ΔPBR, BC = 8 cm, AC = 10 cm , ∠B = 90°, `"BC"/"BR" = 5/4` then construct ∆ABC and ΔPBR
Point P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1. If P lies on the line x - y + 2 = 0, then value of k is ______.
For ∆ABC in which BC = 7.5cm, ∠B =45° and AB - AC = 4, select the correct figure.
Draw the line segment AB = 5cm. From the point A draw a line segment AD = 6cm making an angle of 60° with AB. Draw a perpendicular bisector of AD. Select the correct figure.
The ratio of corresponding sides for the pair of triangles whose construction is given as follows: Triangle ABC of dimensions AB = 4cm, BC = 5 cm and ∠B= 60°.A ray BX is drawn from B making an acute angle with AB.5 points B1, B2, B3, B4 and B5 are located on the ray such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
B4 is joined to A and a line parallel to B4A is drawn through B5 to intersect the extended line AB at A’.
Another line is drawn through A’ parallel to AC, intersecting the extended line BC at C’. Find the ratio of the corresponding sides of ΔABC and ΔA′BC′.
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

