Advertisements
Advertisements
Question
Construct the circumcircle and incircle of an equilateral triangle ABC with side 6 cm and centre O. Find the ratio of radii of circumcircle and incircle.
Solution
Construction:-

Steps of Construction:-
- Construct an equilateral triangle Δ ABC with side 6 cm.
- Draw perpendicular bisectors of any two sides. Let O be the point of intersection.
- Draw a circle with centre O and radius OA or OB or OC. This gives us circumcircle equilateral triangle Δ ABC.
- Draw the bisector of ∠C . It passes through centre of the circle O.
- Draw a circle with radius OM. This gives us incircle of the equilateral triangle Δ ABC.

In an equilateral triangle angle bisector and median are same, also circumcentre and incentre are same. For equilateral triangle circumcentre divides the median in 2:1.
So the ratio of radii of circumcircle and incircle is 2:1.
APPEARS IN
RELATED QUESTIONS
Construct a Δ ABC in which AB = 6 cm, ∠A = 30° and ∠B = 60°, Construct another ΔAB’C’ similar to ΔABC with base AB’ = 8 cm.
Find the ratio in which the line segment joining the points A(3,- 3) and B(- 2, 7) is divided by x-axis. Also find the coordinates of the point of division.
Construct a triangle ABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
Construct an isosceles triangle with base 8 cm and altitude 4 cm. Construct another triangle whose sides are `2/3` times the corresponding sides of the isosceles triangle.
Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to (3/4)th of the corresponding sides of ΔABC.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 5 cm and 4 cm. Then construct another triangle whose sides are 5/3th times the corresponding sides of the given triangle.
Construct a triangle similar to a given ΔXYZ with its sides equal to (3/4)th of the corresponding sides of ΔXYZ. Write the steps of construction.
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that `(AP)/(AB) = 3/5 `.
Construct the circumcircle and incircle of an equilateral ∆XYZ with side 6.5 cm and centre O. Find the ratio of the radii of incircle and circumcircle.
Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm and 8 cm. Then construct another triangle, whose sides are `3/5` times the corresponding sides of the given triangle.
∆AMT ~ ∆AHE. In ∆AMT, AM = 6.3 cm, ∠TAM = 50°, AT = 5.6 cm. `"AM"/"AH" = 7/5`. Construct ∆AHE.
Find the ratio in which point T(–1, 6)divides the line segment joining the points P(–3, 10) and Q(6, –8).
The line segment AB is divided into five congruent parts at P, Q, R and S such that A–P–Q–R–S–B. If point Q(12, 14) and S(4, 18) are given find the coordinates of A, P, R, B.
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that `(AP)/(AB)=3/5`.
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are \[\frac{3}{5}\] times the corresponding sides of the given triangle.
Δ AMT ∼ ΔAHE. In Δ AMT, MA = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `(MA)/(HA) = 7/5`. construct Δ AHE.
Choose the correct alternative:
______ number of tangents can be drawn to a circle from the point on the circle.
Choose the correct alternative:

In the figure ΔABC ~ ΔADE then the ratio of their corresponding sides is ______
ΔPQR ~ ΔABC. In ΔPQR, PQ = 3.6cm, QR = 4 cm, PR = 4.2 cm. Ratio of the corresponding sides of triangle is 3 : 4, then construct ΔPQR and ΔABC
ΔAMT ~ ΔAHE. In ΔAMT, AM = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `"AM"/"HA" = 7/5`, then construct ΔAMT and ΔAHE
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm. ∠D = 30°, ∠N = 20°, `"HP"/"ED" = 4/5`, then construct ΔRHP and ∆NED
If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio
Solution:
Point P divides segment AB in the ratio m: n.
A(8, 9) = (x1, y1), B(1, 2 ) = (x2, y2) and P(6, 7) = (x, y)
Using Section formula of internal division,
∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`
∴ 7m + 7n = `square` + 9n
∴ 7m – `square` = 9n – `square`
∴ `square` = 2n
∴ `"m"/"n" = square`
To divide a line segment AB in the ratio 5 : 6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray BY parallel to AX and the points A1, A2, A3, ... and B1, B2, B3, ... are located at equal distances on ray AX and BY, respectively. Then the points joined are ______.
To construct a triangle similar to a given ΔABC with its sides `8/5` of the corresponding sides of ΔABC draw a ray BX such that ∠CBX is an acute angle and X is on the opposite side of A with respect to BC. Then minimum number of points to be located at equal distances on ray BX is ______.
When a line segment is divided in the ratio 2 : 3, how many parts is it divided into?
Match the following based on the construction of similar triangles, if scale factor `(m/n)` is.
| Column I | Column II | ||
| i | >1 | a) | The similar triangle is smaller than the original triangle. |
| ii | <1 | b) | The two triangles are congruent triangles. |
| iii | =1 | c) | The similar triangle is larger than the original triangle. |
The image of construction of A’C’B a similar triangle of ΔACB is given below. Then choose the correct option.
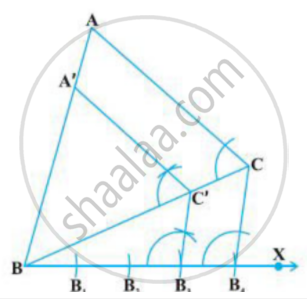
Construction of similar polygons is similar to that of construction of similar triangles. If you are asked to construct a parallelogram similar to a given parallelogram with a given scale factor, which of the given steps will help you construct a similar parallelogram?
A point C divides a line segment AB in the ratio 5 : 6. The ratio of lengths AB: BC is ______.

By geometrical construction, it is possible to divide a line segment in the ratio `sqrt(3) : 1/sqrt(3)`.
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = `3/4` AB and AQ = `1/4` AC. Join P and Q and measure the length PQ.
Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and ∠ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD' C' similar to ∆BDC with scale factor `4/3`. Draw the line segment D'A' parallel to DA where A' lies on extended side BA. Is A'BC'D' a parallelogram?
Draw a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Construct a triangle similar to ∆ABC with scale factor `5/7`. Justify the construction.
Draw a line segment AB of length 10 cm and divide it internally in the ratio of 2:5 Justify the division of line segment AB.
