Advertisements
Advertisements
Question
Construct a triangle similar to a given ΔXYZ with its sides equal to (3/4)th of the corresponding sides of ΔXYZ. Write the steps of construction.
Solution
let XY = cm, YZ = cm and ∠Y = 60° and then a triangle similar to it whose sides are (3/4)th of the corrosponding sides of ΔXYZ
we follow the following steps to construct triangle.
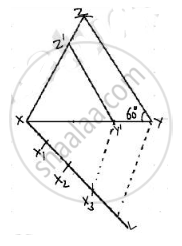
Step of construction
step 1. First of all we draw a line segment XY = 5 cm
step 2. With Y as centre on angle ∠Y = 60°
step 3. with Y as centre and radius YZ = 6 cm, draw on arc
step 4. Join XZ to obtain ΔXYZ
step 5. Below XY1 makes an acute angle ∠YXL = 60°
step 6. Below XL, mark off four points X1, X2, X3 and X4 such that XX1 = X1X2 = X2X3 = X3X4
step 7. Join X4Y
step 8. since we have to construct a triangle each of whose sides is (3/4)th of the corresponding sides of ΔXYZ
So, we take three parts out of four equal parts on XL from point X3 draw X3Y' || X4Y and meeting XY at Y'
step 9. From Y' draw Y'Z' || YZ, and meeting XZ at Z'
Hence, ΔXY'Z' is the required triangle, each of whose sides is (3/4)th of the corresponding sides of ΔXYZ
APPEARS IN
RELATED QUESTIONS
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts. Give the justification of the construction.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are `7/5` of the corresponding sides of the first triangle. Give the justification of the construction.
Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
Draw a right triangle ABC in which AC = AB = 4.5 cm and ∠A = 90°. Draw a triangle similar to ΔABC with its sides equal to (5/4)th of the corresponding sides of ΔABC.
Δ AMT ∼ ΔAHE. In Δ AMT, MA = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `(MA)/(HA) = 7/5`. construct Δ AHE.
Point P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1. If P lies on the line x - y + 2 = 0, then value of k is ______.
To divide a line segment AB in the ratio 5 : 7, first a ray AX is drawn so that ∠BAX is an acute angle and then at equal distances points are marked on the ray AX such that the minimum number of these points is ______.
By geometrical construction, it is possible to divide a line segment in the ratio `sqrt(3) : 1/sqrt(3)`.
Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = `3/4` AB and AQ = `1/4` AC. Join P and Q and measure the length PQ.
Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and ∠ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD' C' similar to ∆BDC with scale factor `4/3`. Draw the line segment D'A' parallel to DA where A' lies on extended side BA. Is A'BC'D' a parallelogram?
