Advertisements
Advertisements
Question
Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm and 8 cm. Then construct another triangle, whose sides are `3/5` times the corresponding sides of the given triangle.
Solution
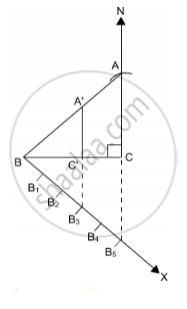
Given:
BC = 6 cm, AC = 8 cm
The triangle to be formed is to be right angled triangle.
Steps of construction:
1. Draw a line segment BC = 6 cm.
2. Draw a ray CN making an angle of 90° at C.
3. With C as centre, taking 8 cm as the radius make an arc at CN intersecting it at A. Join AB.
4. Now, ABC is the triangle whose similar triangle is to be drawn.
5. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
6. Locate 5 (Greater of 3 and 5 in `3/5` ) points B1, B2, B3, B4 and B5 on BX so that BB1= B1B2 = B2B3= B3B4 = B4B5
7. Join B5C and draw a line through B3 (Smaller of 3 and 5 in `3/5` ) parallel to B5C to intersect BC at C’.
8. Draw a line through C’parallel to the line CA to intersect BA at A’.
9. A’BC’ is the required similar triangle whose sides are `3/5` times the corresponding sides of ΔABC.
APPEARS IN
RELATED QUESTIONS
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts. Give the justification of the construction.
Draw a ∆ABC in which AB = 4 cm, BC = 5 cm and AC = 6 cm. Then construct another triangle whose sides are\[\frac{3}{5}\] of the corresponding sides of ∆ABC ?
Δ AMT ∼ ΔAHE. In Δ AMT, MA = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `(MA)/(HA) = 7/5`. construct Δ AHE.
Find the co-ordinates of the centroid of the Δ PQR, whose vertices are P(3, –5), Q(4, 3) and R(11, –4)
Draw seg AB of length 9 cm and divide it in the ratio 3 : 2
A triangle ABC is such that BC = 6cm, AB = 4cm and AC = 5cm. For the triangle similar to this triangle with its sides equal to `3/4`th of the corresponding sides of ΔABC, correct figure is?
To divide a line segment PQ in the ratio 5 : 7, first a ray PX is drawn so that ∠QPX is an acute angle and then at equal distances points are marked on the ray PX such that the minimum number of these points is ______.
Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = `3/4` AB and AQ = `1/4` AC. Join P and Q and measure the length PQ.
Draw a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Construct a triangle similar to ∆ABC with scale factor `5/7`. Justify the construction.
Draw a line segment AB of length 6 cm and mark a point X on it such that AX = `4/5` AB. [Use a scale and compass]
