Advertisements
Advertisements
प्रश्न
Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm and 8 cm. Then construct another triangle, whose sides are `3/5` times the corresponding sides of the given triangle.
उत्तर
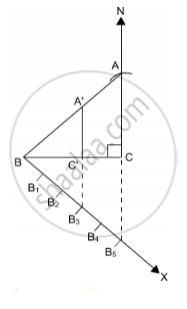
Given:
BC = 6 cm, AC = 8 cm
The triangle to be formed is to be right angled triangle.
Steps of construction:
1. Draw a line segment BC = 6 cm.
2. Draw a ray CN making an angle of 90° at C.
3. With C as centre, taking 8 cm as the radius make an arc at CN intersecting it at A. Join AB.
4. Now, ABC is the triangle whose similar triangle is to be drawn.
5. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
6. Locate 5 (Greater of 3 and 5 in `3/5` ) points B1, B2, B3, B4 and B5 on BX so that BB1= B1B2 = B2B3= B3B4 = B4B5
7. Join B5C and draw a line through B3 (Smaller of 3 and 5 in `3/5` ) parallel to B5C to intersect BC at C’.
8. Draw a line through C’parallel to the line CA to intersect BA at A’.
9. A’BC’ is the required similar triangle whose sides are `3/5` times the corresponding sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
Write down the equation of a line whose slope is 3/2 and which passes through point P, where P divides the line segment AB joining A(-2, 6) and B(3, -4) in the ratio 2 : 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are `7/5` of the corresponding sides of the first triangle. Give the justification of the construction.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are `4/3 `times the corresponding side of ΔABC. Give the justification of the construction.
Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5
If A (20, 10), B(0, 20) are given, find the coordinates of the points which divide segment AB into five congruent parts.
If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio
Solution:
Point P divides segment AB in the ratio m: n.
A(8, 9) = (x1, y1), B(1, 2 ) = (x2, y2) and P(6, 7) = (x, y)
Using Section formula of internal division,
∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`
∴ 7m + 7n = `square` + 9n
∴ 7m – `square` = 9n – `square`
∴ `square` = 2n
∴ `"m"/"n" = square`
To divide a line segment AB in the ratio 4 : 7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1, A2, A3, .... are located at equal distances on the ray AX and the point B is joined to ______.
The point W divides the line XY in the ratio m : n. Then, the ratio of lengths of the line segments XY : WX is ______.
Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and ∠ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD' C' similar to ∆BDC with scale factor `4/3`. Draw the line segment D'A' parallel to DA where A' lies on extended side BA. Is A'BC'D' a parallelogram?
Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 9 cm. Construct a triangle similar to ∆ABC with scale factor `3/2`. Justify the construction. Are the two triangles congruent? Note that all the three angles and two sides of the two triangles are equal.
