Advertisements
Advertisements
प्रश्न
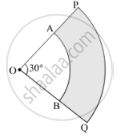
In Fig. 7, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and
3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [User`22/7`]
उत्तर
PQ and AB are the arcs of two concentric circles of radii 7 cm and 3.5 cm respectively.
Let r1and r2 be the radii of the outer and the inner circle respectively.
Suppose θ be the angle subtended by the arcs at the centre O.
Then r1 = 7 cm, r2 = 3.5 cm and θ = 30°
Area of the shaded region
= Area of sector OPQ − Area of sector OAB
`=O//360^@pir_1^2-O//360^@pir_2^2`
`=O//360^@pi(r_1^2-r_2^2)`
`=30^@/360^@xx22/7p[(7cm)^2-(3.5)^2]`
`=1/12xx22/7xx(49-12.25)cm^2`
`=9.625 cm^2`
Thus, the area of the shaded region is 9.625 cm2.
संबंधित प्रश्न
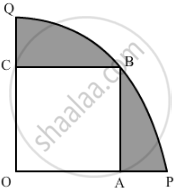
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles. [Use Π = 22/7]
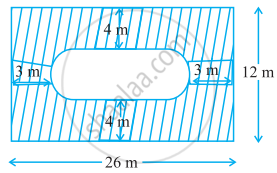
The given figure depicts a racing track whose left and right ends are semicircular.
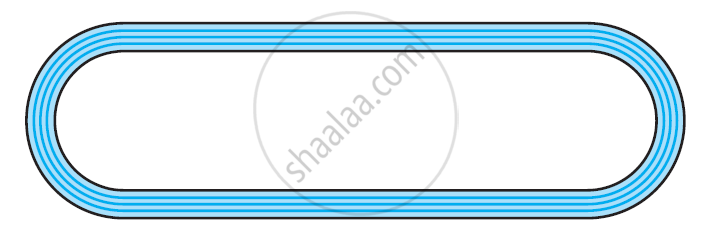
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[Use Π = 22/7]
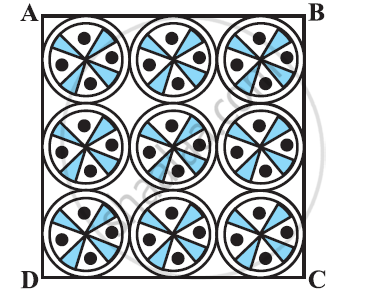
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the given figure). Find the area of the remaining portion of the handkerchief.[Use Π = 22/7]
The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at ₹ 40 per `m^2`
The difference between the sides at the right angles in a right-angled triangle is 7 cm. the area of the triangle is `60 cm^2` . Find its perimeter.
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
The height of an equilateral triangle is 6 cm. Find its area.
In Fig.5, AB and CD are two diameters of a circle with centre O, which are perpendicular to each other. OB is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. `[\text{Use}pi=22/7]`
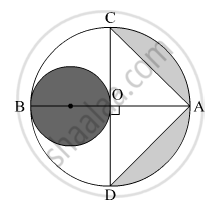
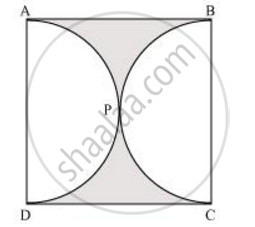
Find the area of the shaded region in figure.