Advertisements
Advertisements
Question
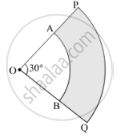
In Fig. 7, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and
3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [User`22/7`]
Solution
PQ and AB are the arcs of two concentric circles of radii 7 cm and 3.5 cm respectively.
Let r1and r2 be the radii of the outer and the inner circle respectively.
Suppose θ be the angle subtended by the arcs at the centre O.
Then r1 = 7 cm, r2 = 3.5 cm and θ = 30°
Area of the shaded region
= Area of sector OPQ − Area of sector OAB
`=O//360^@pir_1^2-O//360^@pir_2^2`
`=O//360^@pi(r_1^2-r_2^2)`
`=30^@/360^@xx22/7p[(7cm)^2-(3.5)^2]`
`=1/12xx22/7xx(49-12.25)cm^2`
`=9.625 cm^2`
Thus, the area of the shaded region is 9.625 cm2.
RELATED QUESTIONS
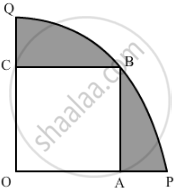
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
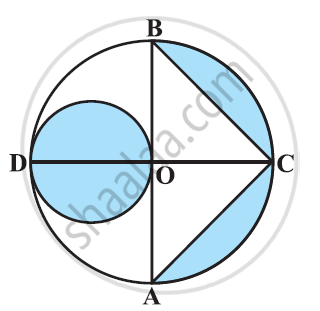
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. [Use Π = 22/7]
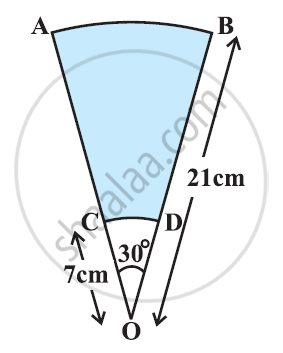
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
Find the area of triangle whose base measures 24 cm and the corresponding height measure 14.5 cm.
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
The height of an equilateral triangle is 6 cm. Find its area.
If the area of an equilateral triangle is `36sqrt3 cm^2` find its perimeter.
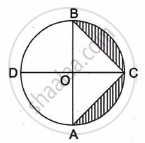
In the given figure, AB and CD are diameters of a circle with centre O perpendicular to each other. If OA = 7 cm, find the area of shaded region.