Advertisements
Advertisements
Question
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
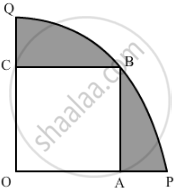
Solution
Let us join OB.
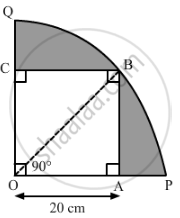
In ΔOAB:
OB2 = OA2 + AB2 = (20)2 + (20)2 = 2 × (20)2
⇒ OB = 20 √2
Radius of the circle, r = `20 sqrt2` cm
`"Area of qudrant OBPQ"=90^@/360^@xx3.14xx(20sqrt2)^2`
`=90/360xx3.14xx(20sqrt2)^2 cm^2`
`=1/4xx3.14xx800 cm^2`
`=628 cm^2`
Area of square OABC = (Side)2 = (20)2 cm2 = 400 cm2
∴ Area of the shaded region = Area of quadrant OPBQ − Area of square OA
= (628 − 400) cm2
= 228 cm2
APPEARS IN
RELATED QUESTIONS
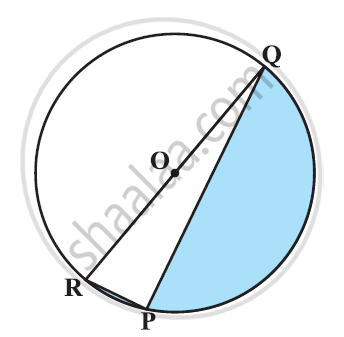
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle. [Use Π = 22/7]
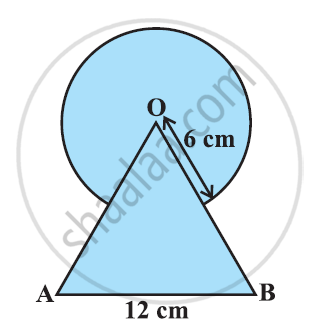
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
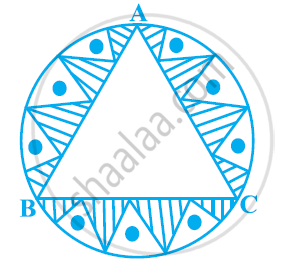
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
The given figure depicts a racing track whose left and right ends are semicircular.
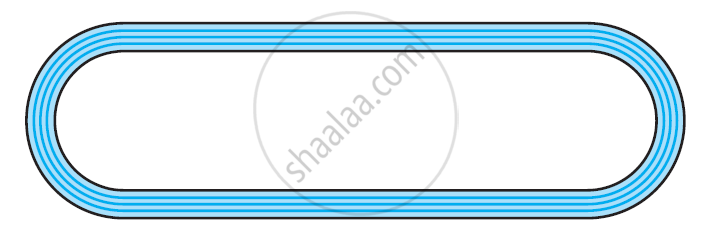
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[Use Π = 22/7]
Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each. [Use Π = 22/7]

The radii of two circles are 19cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of circumference of two circles.
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
The sides of a triangle are in the ratio 5:12:13 and its perimeter is 150 m. Find the area of the triangle.
The height of an equilateral triangle is 6 cm. Find its area.
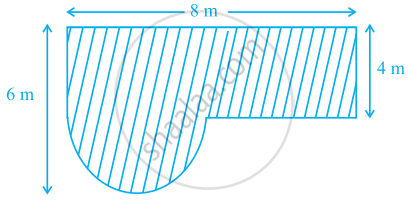
Find the area of the shaded field shown in figure.