Advertisements
Advertisements
Question
Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each. [Use Π = 22/7]

Solution
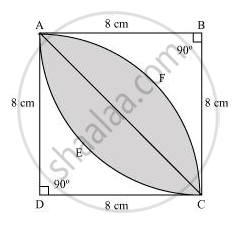
The designed area is the common region between two sectors BAEC and DAFC.
Area of sector BAEC = `90^@/360^@ xx 22/7xx(8)^2`
`=1/4xx22/7xx64`
`=(22xx16)/7 cm^2`
`= 352/7 cm^2`
Area of ΔBAC = `1/2xxBAxxBC`
`= 1/2xx8xx7 = 32 cm^2`
Area of the designed portion = 2 × (Area of segment AEC)
= 2 × (Area of sector BAEC − Area of ΔBAC)
`= 2xx(352/7 - 32) = 2((352-224)/4)`
`= (2xx128)/7`
`= 256/7 cm^2`
APPEARS IN
RELATED QUESTIONS
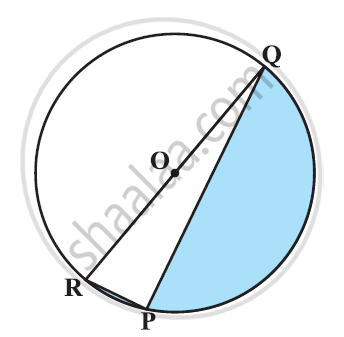
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle. [Use Π = 22/7]
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

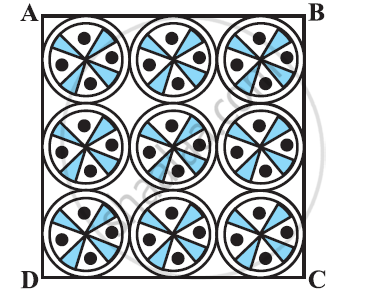
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the given figure). Find the area of the remaining portion of the handkerchief.[Use Π = 22/7]
If the area of an equilateral triangle is `36sqrt3 cm^2` find its perimeter.
Find the area of shaded region in Fig. 4, where a circle of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm. (Use π = 3.14 and\[\sqrt{3}\] =1.73)
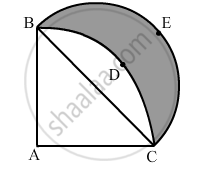
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
Find the area of the flower bed (with semi-circular ends) shown in figure.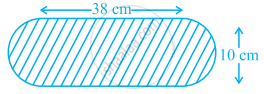
Read the following passage:
|
For the inauguration of 'Earth day' week in a school, badges were given to volunteers. Organisers purchased these badges from an NGO, who made these badges in the form of a circle inscribed in a square of side 8 cm.
|
Based on the above information, answer the following questions:
- What is the area of square ABCD?
- What is the length of diagonal AC of square ABCD?
- Find the area of sector OPRQO.
OR
Find the area of remaining part of square ABCD when area of circle is excluded.
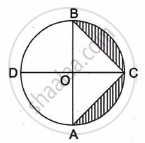
In the given figure, AB and CD are diameters of a circle with centre O perpendicular to each other. If OA = 7 cm, find the area of shaded region.