Advertisements
Advertisements
Question
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
Solution
Let the usual speed of the plane be x km/hr
And the new speed of the plane after increased by 250 is `(x + 250)` km/hr
According to question
`1500/x - 1500/((x + 250)) = 30/60`
⇒ `(1500x + 1500 xx 250 - 1500x)/(x(x + 250)) = 1/2`
⇒ `1500 xx 250 xx 2 = x(x + 250)`
⇒ `750000 = x^2 + 250x`
⇒ `x^2 + 1000x - 750x - 750000 = 0`
⇒ `(x + 1000)(x - 750) = 0`
x = 750, - 1000
Speed can not be negative so -1000 will be neglected
Therefore, usual speed of the plane is 750 km/hr.
APPEARS IN
RELATED QUESTIONS
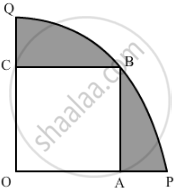
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
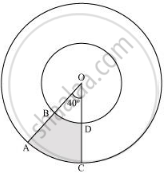
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40° [Use Π = 22/7]
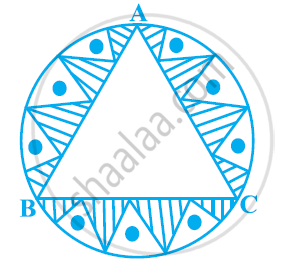
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
Find the area of triangle whose base measures 24 cm and the corresponding height measure 14.5 cm.
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
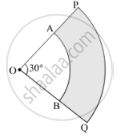
In Fig. 7, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and
3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [User`22/7`]
In Figure 4, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. (Use π = 3.14)
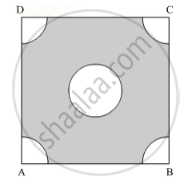
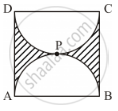
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`
Read the following passage:
|
For the inauguration of 'Earth day' week in a school, badges were given to volunteers. Organisers purchased these badges from an NGO, who made these badges in the form of a circle inscribed in a square of side 8 cm.
|
Based on the above information, answer the following questions:
- What is the area of square ABCD?
- What is the length of diagonal AC of square ABCD?
- Find the area of sector OPRQO.
OR
Find the area of remaining part of square ABCD when area of circle is excluded.


