Advertisements
Advertisements
Question
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
Solution
Radius of outer circle = 21𝑐𝑚
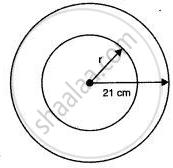
Radius of inner circle = 𝑅2
Area between concentric circles = area of outer circle – area of inner circle
⇒ 770 =`22/7`(212 − R22)
⇒ 212 − 𝑅22 = 35 × 7 = 245
⇒ 441 – 245 = 𝑅22
⇒𝑅2= `sqrt(196)` = 14 𝑐𝑚
Radius of inner circle = 14cm.
APPEARS IN
RELATED QUESTIONS
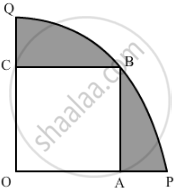
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

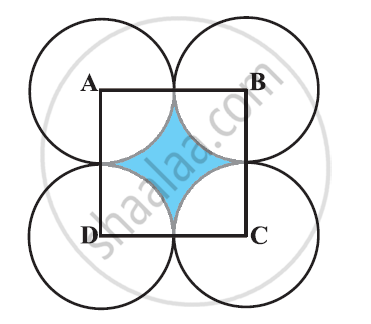
In the given figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region. [Use Π = 22/7]
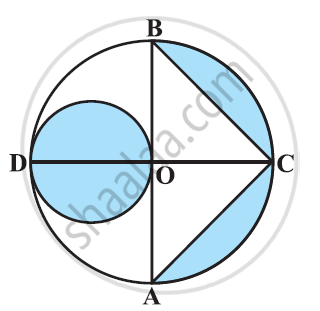
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. [Use Π = 22/7]
In the given figure, OACB is a quadrant of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) Quadrant OACB
(ii) Shaded region
[Use Π = 22/7]

If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
The radii of two circles are 19cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of circumference of two circles.
In Figure 4, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. (Use π = 3.14)
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
Read the following passage:
Governing council of a local public development authority of Dehradun decided to build an adventurous playground on the top of a hill, which will have adequate space for parking.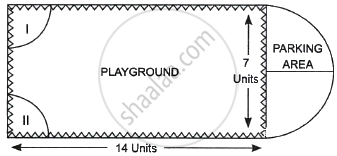 After survey, it was decided to build rectangular playground, with a semi-circular area allotted for parking at one end of the playground. The length and breadth of the rectangular playground are 14 units and 7 units, respectively. There are two quadrants of radius 2 units on one side for special seats. |
Based on the above information, answer the following questions:
- What is the total perimeter of the parking area?
- (a) What is the total area of parking and the two quadrants?
OR
(b) What is the ratio of area of playground to the area of parking area? - Find the cost of fencing the playground and parking area at the rate of ₹ 2 per unit.
