Advertisements
Advertisements
Question
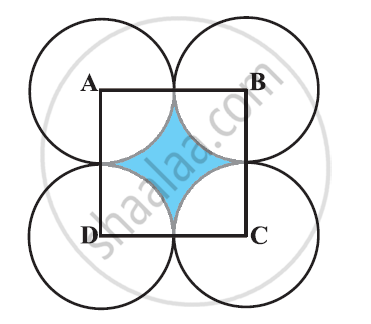
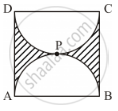
In the given figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region. [Use Π = 22/7]
Solution

Area of each of the 4 sectors is equal to each other and is a sector of 90° in a circle of 7 cm radius.
Area of each sector = `90^@/360^@ xx pi(7)^2`
`=1/4xx22/7xx7xx7`
`= 77/2 cm^2`
Area of square ABCD = (Side)2 = (14)2 = 196 cm2
Area of shaded portion = Area of square ABCD − 4 × Area of each sector
`196 - 4 xx 77/2 = 196 - 154`
`= 42 cm^2`
Therefore, the area of shaded portion is 42 cm2.
APPEARS IN
RELATED QUESTIONS
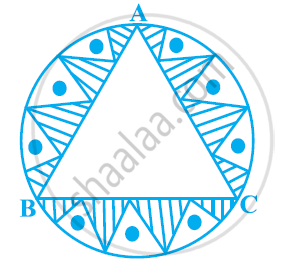
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
The given figure depicts a racing track whose left and right ends are semicircular.
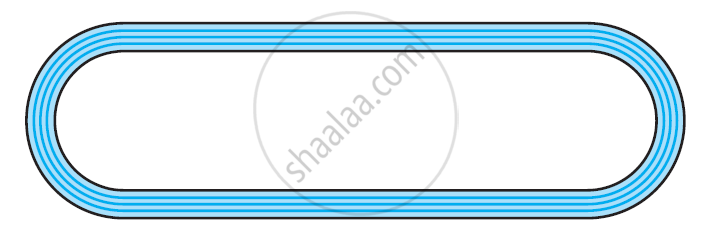
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[Use Π = 22/7]
In the given figure, OACB is a quadrant of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) Quadrant OACB
(ii) Shaded region
[Use Π = 22/7]

Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each. [Use Π = 22/7]

The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at ₹ 40 per `m^2`
If the area of an equilateral triangle is `81sqrt3 cm^2` find its height.
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
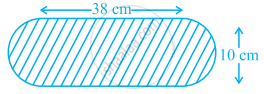
Find the area of the flower bed (with semi-circular ends) shown in figure.