Advertisements
Advertisements
Question
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
Solution
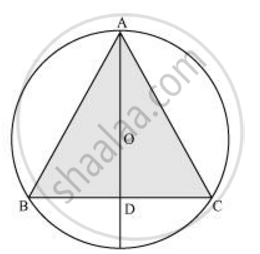
Radius (r) of circle = 32 cm
AD is the median of ΔABC.
`AO =2/3 AD = 32`
AD = 48 cm
In ΔABD,
AB2 = AD2 + BD2
`AB^2 = (48)^2 + ((AB)/2)^2`
`(3AB^2)/4 = (48)^2`
`AB = (48xx2)/sqrt3 = 96/sqrt3`
`= 32sqrt3 cm`
Area of equilateral triangle ΔABC = `sqrt3/4(32sqrt3)^2`
`=sqrt3/4 xx 32xx32xx2 = 96xx8xxsqrt3`
`= 768sqrt3 cm^2`
Area of circle = πr2
`= 22/7xx(32)^2`
`=22/7 xx 1024`
`= 22528/7 cm^2`
Area of design = Area of circle − Area of ΔABC
`= ((22528)/7 - 768sqrt3) cm^2`
APPEARS IN
RELATED QUESTIONS
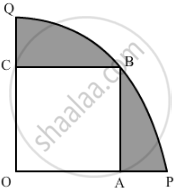
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
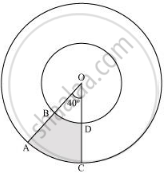
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40° [Use Π = 22/7]
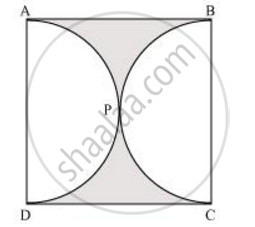
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles. [Use Π = 22/7]
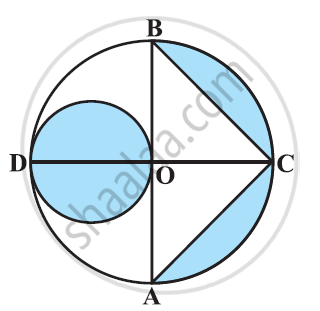
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. [Use Π = 22/7]
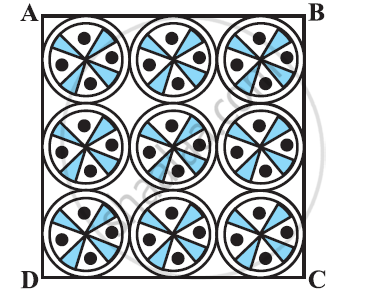
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the given figure). Find the area of the remaining portion of the handkerchief.[Use Π = 22/7]
A park is in the form of rectangle 120m × 100m. At the centre of park there is a circular lawn. The area of park excluding lawn is 8700m2. Find the radius of circular lawn.
Find the area of triangle whose base measures 24 cm and the corresponding height measure 14.5 cm.
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
Find the area of the shaded region in figure.