Advertisements
Advertisements
प्रश्न
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
उत्तर
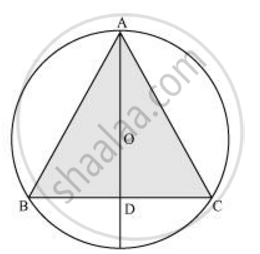
Radius (r) of circle = 32 cm
AD is the median of ΔABC.
`AO =2/3 AD = 32`
AD = 48 cm
In ΔABD,
AB2 = AD2 + BD2
`AB^2 = (48)^2 + ((AB)/2)^2`
`(3AB^2)/4 = (48)^2`
`AB = (48xx2)/sqrt3 = 96/sqrt3`
`= 32sqrt3 cm`
Area of equilateral triangle ΔABC = `sqrt3/4(32sqrt3)^2`
`=sqrt3/4 xx 32xx32xx2 = 96xx8xxsqrt3`
`= 768sqrt3 cm^2`
Area of circle = πr2
`= 22/7xx(32)^2`
`=22/7 xx 1024`
`= 22528/7 cm^2`
Area of design = Area of circle − Area of ΔABC
`= ((22528)/7 - 768sqrt3) cm^2`
APPEARS IN
संबंधित प्रश्न
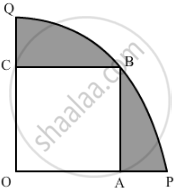
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
The given figure depicts a racing track whose left and right ends are semicircular.
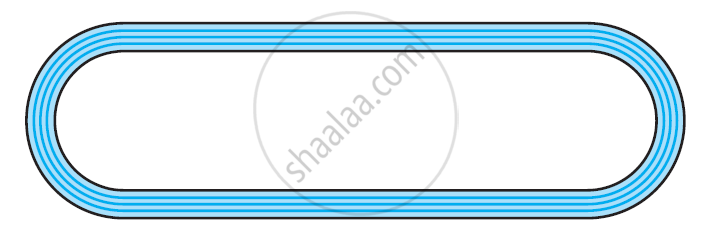
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[Use Π = 22/7]
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

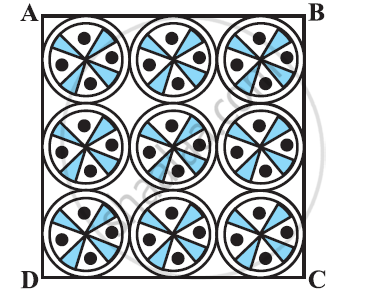
On a square handkerchief, nine circular designs each of radius 7 cm are made (see the given figure). Find the area of the remaining portion of the handkerchief.[Use Π = 22/7]
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. [Use Π = 22/7]

Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each. [Use Π = 22/7]

The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at ₹ 40 per `m^2`
Find the area of triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
Find the area of the flower bed (with semi-circular ends) shown in figure.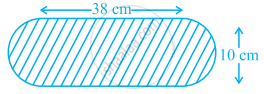
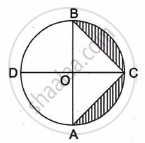
In the given figure, AB and CD are diameters of a circle with centre O perpendicular to each other. If OA = 7 cm, find the area of shaded region.