Advertisements
Advertisements
प्रश्न
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
उत्तर
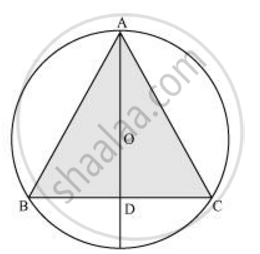
Radius (r) of circle = 32 cm
AD is the median of ΔABC.
`AO =2/3 AD = 32`
AD = 48 cm
In ΔABD,
AB2 = AD2 + BD2
`AB^2 = (48)^2 + ((AB)/2)^2`
`(3AB^2)/4 = (48)^2`
`AB = (48xx2)/sqrt3 = 96/sqrt3`
`= 32sqrt3 cm`
Area of equilateral triangle ΔABC = `sqrt3/4(32sqrt3)^2`
`=sqrt3/4 xx 32xx32xx2 = 96xx8xxsqrt3`
`= 768sqrt3 cm^2`
Area of circle = πr2
`= 22/7xx(32)^2`
`=22/7 xx 1024`
`= 22528/7 cm^2`
Area of design = Area of circle − Area of ΔABC
`= ((22528)/7 - 768sqrt3) cm^2`
APPEARS IN
संबंधित प्रश्न
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. [Use Π = 22/7]

If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
The sides of a triangle are in the ratio 5:12:13 and its perimeter is 150 m. Find the area of the triangle.
The difference between the sides at the right angles in a right-angled triangle is 7 cm. the area of the triangle is `60 cm^2` . Find its perimeter.
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
The area of the square that can be inscribed in a circle of radius 8 cm is ______.
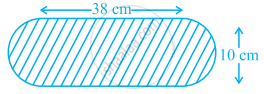
Find the area of the flower bed (with semi-circular ends) shown in figure.