Advertisements
Advertisements
प्रश्न
The area of the square that can be inscribed in a circle of radius 8 cm is ______.
विकल्प
256 cm2
128 cm2
`64sqrt(2)` cm2
64 cm2
उत्तर
The area of the square that can be inscribed in a circle of radius 8 cm is 128 cm2.
Explanation:
Given, radius of circle, r = OC = 8 cm.
∴ Diameter of the circle = AC
= 2 × OC
= 2 × 8
= 16 cm
Which is equal to the diagonal of a square.
Let side of square be x.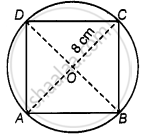
In right-angled ΔABC,
AC2 = AB2 + BC2 ...[By Pythagoras theorem]
⇒ (16)2 = x2 + x2
⇒ 256 = 2x2
⇒ x2 = 128
∴ Area of square = x2 = 128 cm2
APPEARS IN
संबंधित प्रश्न
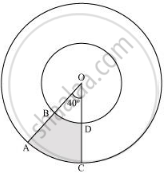
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40° [Use Π = 22/7]
The given figure depicts a racing track whose left and right ends are semicircular.
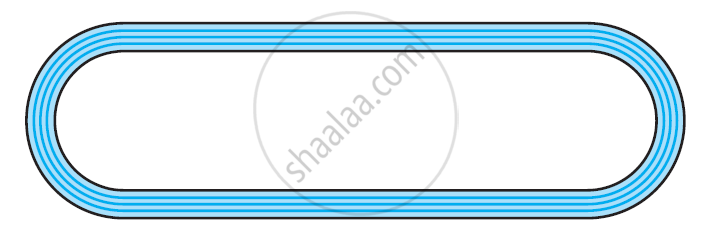
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[Use Π = 22/7]
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

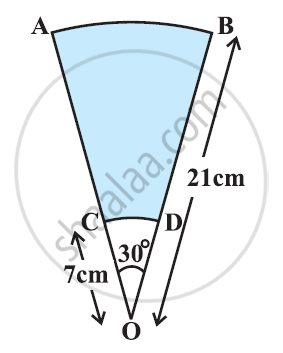
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
The radii of two circles are 19cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of circumference of two circles.
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
