Advertisements
Advertisements
प्रश्न
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
उत्तर
Let the usual speed of the plane be x km/hr
And the new speed of the plane after increased by 250 is `(x + 250)` km/hr
According to question
`1500/x - 1500/((x + 250)) = 30/60`
⇒ `(1500x + 1500 xx 250 - 1500x)/(x(x + 250)) = 1/2`
⇒ `1500 xx 250 xx 2 = x(x + 250)`
⇒ `750000 = x^2 + 250x`
⇒ `x^2 + 1000x - 750x - 750000 = 0`
⇒ `(x + 1000)(x - 750) = 0`
x = 750, - 1000
Speed can not be negative so -1000 will be neglected
Therefore, usual speed of the plane is 750 km/hr.
APPEARS IN
संबंधित प्रश्न
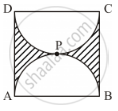
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles. [Use Π = 22/7]
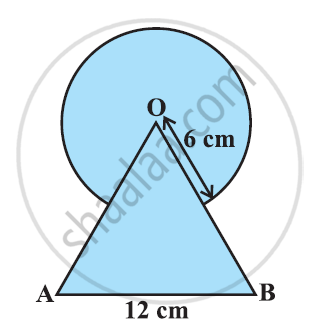
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
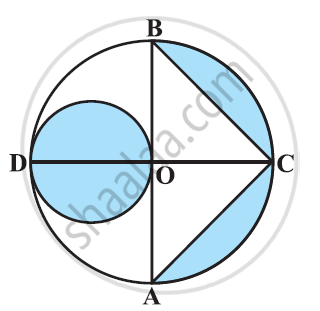
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. [Use Π = 22/7]
The radii of two circles are 19cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of circumference of two circles.
Find the area of triangle whose base measures 24 cm and the corresponding height measure 14.5 cm.
The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
The height of an equilateral triangle is 6 cm. Find its area.
Find the area of shaded region in Fig. 4, where a circle of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm. (Use π = 3.14 and\[\sqrt{3}\] =1.73)
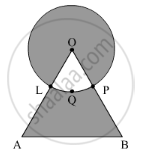
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
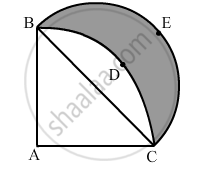
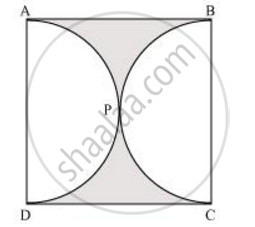
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`