Advertisements
Advertisements
प्रश्न
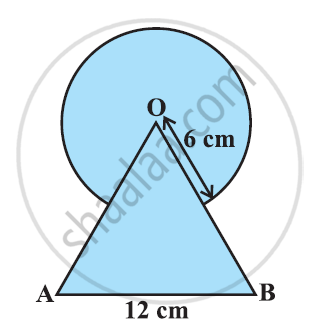
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
उत्तर
We know that each interior angle of an equilateral triangle is of measure 60°.
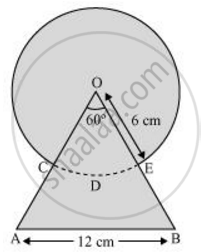
Area of sector OCDE = `60^@/360^@pir^2`
`=1/6xx22/7xx6xx6`
`= 132/7 cm^2`
Area of triangleOAB = `sqrt3/4(12)^2 = (sqrt3xx12xx12)/4 = 36sqrt3 cm^2`
Area of circle = `pir^2 = 22/7xx6xx6 = 792/7 cm^2`
Area of shaded region = Area of ΔOAB + Area of circle − Area of sector OCDE
`= 36sqrt3 + 792/7 - 132/7`
`=(36sqrt3 + 660/7) cm^2`
APPEARS IN
संबंधित प्रश्न
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. [Use Π = 22/7]
In the given figure, OACB is a quadrant of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) Quadrant OACB
(ii) Shaded region
[Use Π = 22/7]

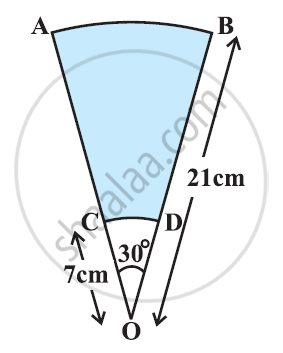
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
Find the areas of the triangle whose sides are 42 cm, 34 cm and 20 cm. Also, find the height corresponding to the longest side.
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
The height of an equilateral triangle is 6 cm. Find its area.
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away on time, it has to increase its speed by 250 km/hr from its usual speed. Find the usual speed of the plane.
Find the area of the shaded field shown in figure.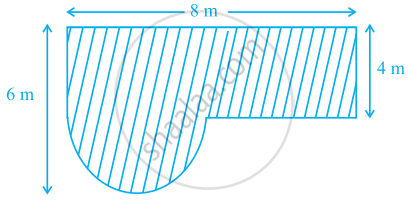
Find the area of the shaded region in figure.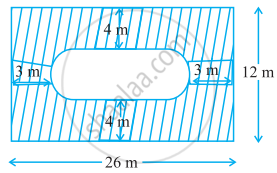
In the given figure, AB and CD are diameters of a circle with centre O perpendicular to each other. If OA = 7 cm, find the area of shaded region.