Advertisements
Advertisements
प्रश्न
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
उत्तर
The perimeter of a right-angled triangle = 40 cm
therfore,` a+b+c=40`
Hypotenuse = 17 cm
Therefore, c = 17cm
`a+b+c=40 cm`
⇒`a+b+17=40`
⇒` a+b=23`
⇒`b=23-a ` .................(1)
Now, using Pythagoras theorem, we have:
`a^2+b^2=c^2`
⇒ `a^2+(23-a)^2=17^2`
⇒` a^2+529-46a+a^2=289`
⇒` 2a^2-46a+529-289=0`
⇒`2a^2-46a+240=0`
⇒` a^2-23a+120=0`
⇒`(a-15) (a-8)=0`
⇒a=15 or a=8
Substituting the value of a=15, in equation (i) we get:
`b=23-a`
=`23-15`
=`8 cm`
If we had chosen 8, a cm, then, `b=23-8=15 cm`
In any case,
`"Area of triangle"=1/2xx"Base"xx"height"`
=`1/2xx8xx15`
=`60 cm^2`
APPEARS IN
संबंधित प्रश्न
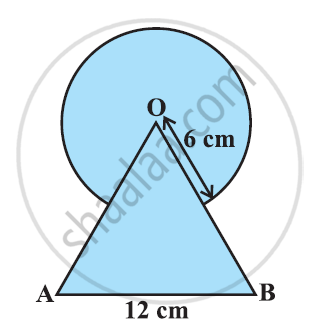
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
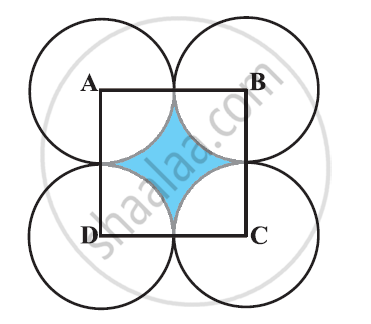
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]

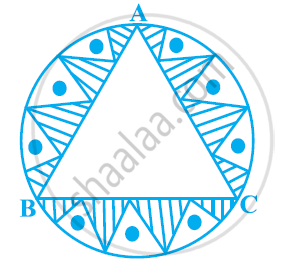
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure. Find the area of the design (Shaded region). [Use Π = 22/7]
In the given figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region. [Use Π = 22/7]
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (See the given figure). Find the area of shaded region. [Use π = 3.14 and `sqrt3 `= 1.73205]

In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. [Use Π = 22/7]

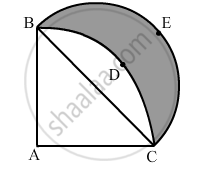
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
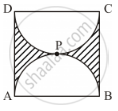
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`
Find the area of the shaded field shown in figure.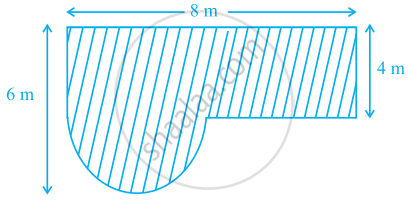
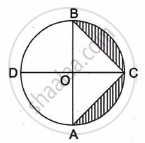
In the given figure, AB and CD are diameters of a circle with centre O perpendicular to each other. If OA = 7 cm, find the area of shaded region.