Advertisements
Advertisements
प्रश्न
The perimeter of a right triangle is 40 cm and its hypotenuse measure 17 cm. Find the area of the triangle.
उत्तर
The perimeter of a right-angled triangle = 40 cm
therfore,` a+b+c=40`
Hypotenuse = 17 cm
Therefore, c = 17cm
`a+b+c=40 cm`
⇒`a+b+17=40`
⇒` a+b=23`
⇒`b=23-a ` .................(1)
Now, using Pythagoras theorem, we have:
`a^2+b^2=c^2`
⇒ `a^2+(23-a)^2=17^2`
⇒` a^2+529-46a+a^2=289`
⇒` 2a^2-46a+529-289=0`
⇒`2a^2-46a+240=0`
⇒` a^2-23a+120=0`
⇒`(a-15) (a-8)=0`
⇒a=15 or a=8
Substituting the value of a=15, in equation (i) we get:
`b=23-a`
=`23-15`
=`8 cm`
If we had chosen 8, a cm, then, `b=23-8=15 cm`
In any case,
`"Area of triangle"=1/2xx"Base"xx"height"`
=`1/2xx8xx15`
=`60 cm^2`
APPEARS IN
संबंधित प्रश्न
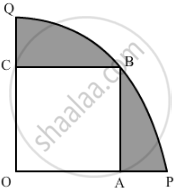
In fig. 3, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
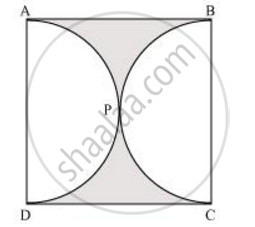
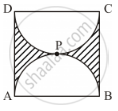
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles. [Use Π = 22/7]
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also find the height corresponding to the smallest side.
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
If the area of an equilateral triangle is `36sqrt3 cm^2` find its perimeter.
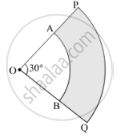
In Fig. 7, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and
3.5 cm and centre O. If ∠POQ = 30°, then find the area of the shaded region. [User`22/7`]
Find the perimeter of the shaded region in Figure 4, if ABCD is a square of side 14 cm and APB and CPD are semicircles. Use `pi = 22/7`
Find the area of triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
Find the area of the shaded region in figure.