Advertisements
Advertisements
प्रश्न
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
उत्तर
(1)The area of the equilateral triangle=`sqrt3/4xx"side"^2`
=`sqrt3/4xx10^2`
=`sqrt3/4xx100`
=`25sqrt3 cm^2`
or `25xx1.732=43.3cm^2`
So, the area of the triangle is `25sqrt3 cm^2 or 433cm^2`
(2) As, area of the equilateral triangle =`25sqrt3 cm^2`
⇒`1/2xx "Base" xx "Height"=25sqrt3`
⇒` 1/2xx10xx"Height"=25sqrt3`
⇒ `5xx"Height"=25sqrt3`
⇒`"Height" =(25sqrt3)/5=5sqrt3`
Or `"Height" = 5xx1.732=8.66m`
∴ The height of the triangle is `5sqrt3 cm or 8.66 cm`
APPEARS IN
संबंधित प्रश्न
The radii of two circles are 19cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of circumference of two circles.
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
Find the areas of the triangle whose sides are 42 cm, 34 cm and 20 cm. Also, find the height corresponding to the longest side.
The sides of a triangle are in the ratio 5:12:13 and its perimeter is 150 m. Find the area of the triangle.
The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
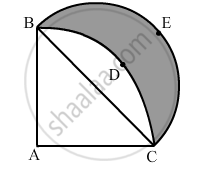
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
Find the area of triangle formed by joining the mid-points of the sides of the triangle whose vertices are A(2, 1), B(4, 3) and C(2, 5).
The area of the square that can be inscribed in a circle of radius 8 cm is ______.
Find the area of the flower bed (with semi-circular ends) shown in figure.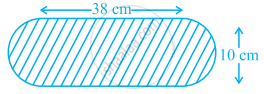
Find the area of the shaded field shown in figure.