Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The radii of two circles are 19cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of circumference of two circles.
рдЙрддреНрддрд░
Radius of 1st circle = 19cm
Radius of 2nd circle = 9 cm
Circumference of 1st circle = 2(19) = 38ЁЭЬЛ cm
Circumference of 2nd circle = 2ЁЭЬЛ (9) = 18ЁЭЬЛ cm
Let radius of required circle = R cm
Circumference of required circle = 2ЁЭЬЛR = ЁЭСР1 + ЁЭСР2
2ЁЭЬЛR = 38ЁЭЬЛ + 18ЁЭЬЛ
2ЁЭЬЛR = 56ЁЭЬЛ
R = 28 cms
Area of required circle = ЁЭЬЛr2
=`22/7× 28 × 28`
= 2464 ЁЭСРЁЭСЪ2
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
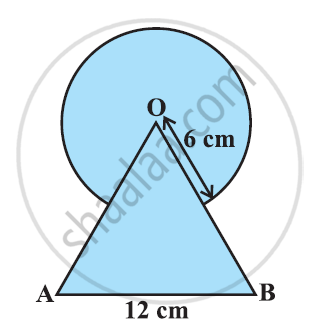
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre [Use Π = 22/7]
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the area of the remaining portion of the square [Use Π = 22/7]
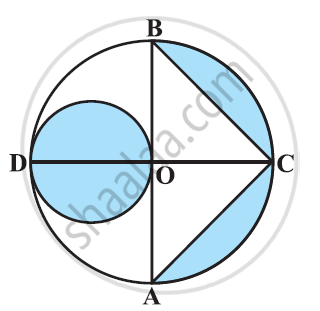
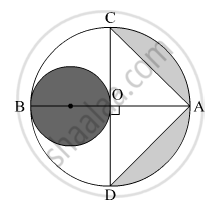
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. [Use Π = 22/7]
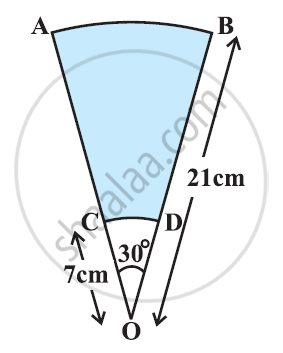
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see the given figure). If ∠AOB = 30°, find the area of the shaded region. [Use Π = 22/7]
Calculate the area of the designed region in the given figure common between the two quadrants of circles of radius 8 cm each. [Use Π = 22/7]
Find the area of triangle whose base measures 24 cm and the corresponding height measure 14.5 cm.
The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
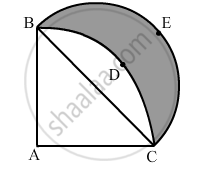
In Figure 5, ABCD is a quadrant of a circle of radius 28 cm and a semi circle BEC is drawn with BC as diameter. Find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
In Fig.5, AB and CD are two diameters of a circle with centre O, which are perpendicular to each other. OB is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. `[\text{Use}pi=22/7]`
The area of the square that can be inscribed in a circle of radius 8 cm is ______.
