Advertisements
Advertisements
рдкреНрд░рд╢реНрди
A car travels 1 km distance in which each wheel makes 450 complete revolutions. Find the radius of wheel.
рдЙрддреНрддрд░
Let radius of wheel = ‘r’ m
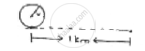
Circumference of wheel = (2ЁЭЬЛr)m.
No. of revolutions = 450
Distance for 450 revolutions = 450 × 2ЁЭЬЛЁЭСЯ = 900ЁЭЬЛЁЭСЯ ЁЭСЪ
distance travelled = 1000 m.
900ЁЭЬЛr = 1000
r = 10000 9ЁЭЬЛ × 100
`=10/(9pi)` ЁЭСЪ
=`1000/(9pi)` ЁЭСРЁЭСЪЁЭСа
ЁЭСЯЁЭСОЁЭССЁЭСЦЁЭСвЁЭСа (ЁЭСЯ) =`1000/(9pi)`ЁЭСРЁЭСЪЁЭСа
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
An arc of a circle is of length 5π cm and the sector it bounds has an area of 20 π cm2. Find the radius of the circle.
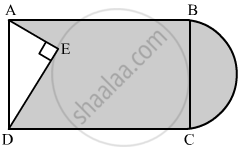
In the given figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π = 3.14]
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 8 cm , diameter = 12 cm
Find the area and perimeter of the following semi-circle :
Diameter= 7 cm
A wheel has a diameter of 84 cm. Find how many completer revolutions must it make to cover 3.168 km.
The perimeter of a square and the circumference of a circle are equal. If the length of each side of the square is 22 cm, find:
(i) perimeter of the square.
(ii) circumference of the circle.
(iii) radius of the circle.
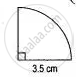
In the adjoining figure, the radius is 3.5 cm. Find:
(i) The area of the quarter of the circle correct to one decimal place.
(ii) The perimeter of the quarter of the circle correct to one decimal place. ( Take π = `22/7`)
The cost of fencing a circular field at the rate of Rs.250 per metre is Rs.55000. The field is to be ploughing at the rate of Rs.15 per m2. Find the cost of ploughing the field.
The radii of the two circles are 19 cm and 9 cm respectively. The radius of the circle which has a circumference equal to the sum of the circumference of two circles is ____________.
Circumferences of two circles are equal. Is it necessary that their areas be equal? Why?
