Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The area enclosed between the concentric circles is 770cm2. If the radius of outer circle 21cm. find the radius of inner circle
рдЙрддреНрддрд░
Radius of outer circle = 21ЁЭСРЁЭСЪ
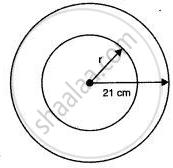
Radius of inner circle = ЁЭСЕ2
Area between concentric circles = area of outer circle – area of inner circle
⇒ 770 =`22/7`(212 − R22)
⇒ 212 − ЁЭСЕ22 = 35 × 7 = 245
⇒ 441 – 245 = ЁЭСЕ22
⇒ЁЭСЕ2= `sqrt(196)` = 14 ЁЭСРЁЭСЪ
Radius of inner circle = 14cm.
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
In the given figure, OACB is a quadrant of circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) Quadrant OACB
(ii) Shaded region
[Use Π = 22/7]
If a square is inscribed in a circle, find the ratio of areas of the circle and the square.
The radii of two circles are 19cm and 9 cm respectively. Find the radius and area of the circle which has circumferences is equal to sum of circumference of two circles.
The perimeter of a triangular field is 240m, and its sides are in the ratio 25:17:12. Find the area of the field. Also, find the cost of ploughing the field at тВ╣ 40 per `m^2`
The length of the two sides of a right triangle containing the right angle differ by 2 cm. If the area of the triangle is 24xm^2, find the perimeter of the triangle.
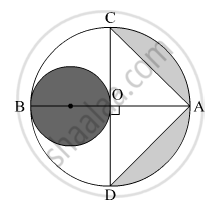
In Fig.5, AB and CD are two diameters of a circle with centre O, which are perpendicular to each other. OB is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region. `[\text{Use}pi=22/7]`
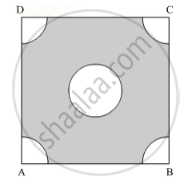
In Figure 4, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region. (Use π = 3.14)
The area of the square that can be inscribed in a circle of radius 8 cm is ______.
Read the following passage:
Governing council of a local public development authority of Dehradun decided to build an adventurous playground on the top of a hill, which will have adequate space for parking.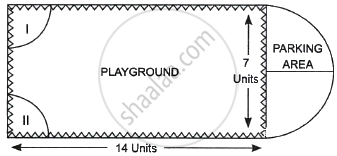 After survey, it was decided to build rectangular playground, with a semi-circular area allotted for parking at one end of the playground. The length and breadth of the rectangular playground are 14 units and 7 units, respectively. There are two quadrants of radius 2 units on one side for special seats. |
Based on the above information, answer the following questions:
- What is the total perimeter of the parking area?
- (a) What is the total area of parking and the two quadrants?
OR
(b) What is the ratio of area of playground to the area of parking area? - Find the cost of fencing the playground and parking area at the rate of тВ╣ 2 per unit.
Read the following passage:
|
For the inauguration of 'Earth day' week in a school, badges were given to volunteers. Organisers purchased these badges from an NGO, who made these badges in the form of a circle inscribed in a square of side 8 cm.
|
Based on the above information, answer the following questions:
- What is the area of square ABCD?
- What is the length of diagonal AC of square ABCD?
- Find the area of sector OPRQO.
OR
Find the area of remaining part of square ABCD when area of circle is excluded.
