Advertisements
Advertisements
प्रश्न
An archery target has three regions formed by three concentric circles as shown in figure. If the diameters of the concentric circles are in the ratios 1 : 2 : 3, then find the ratio of the areas of three regions.
उत्तर

Let the three regions be A, B and C.
The diameters are in the ratio 1 : 2 : 3.
Let the diameters be 1x, 2x and 3x
Then the radius will be `x/2, (2x)/2` and `(3x)/2`
Area of region A = `pi"r"_"A"^2`
= `pi(x/2)^2`
= `pix^2/4`
Area of region B = `pi"r" _"B"^2-pi"r" _"A"^2`
= `pi(x)^2-pi(x/2)^2`
= `(3pi(x)^2)/4`
Area of region C = `pi"r"_"C"^2-pi"r"_"B"^2-pi"r"_"A"^2`
= `pi((3x)/2)^2-pi(x)^2-pi(x/2)^2`
= `pi((3x)/2)^2-(3pix^2)/4`
= `(5pix^2)/4`
Thus, ratio of the areas of regions A, B and C will be
`pix^2/4 : (3pi(x)^2)/4 : (5pix^2)/4`
⇒ 1 : 3 : 5
संबंधित प्रश्न
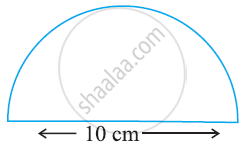
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
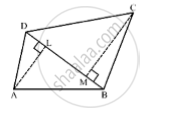
In the given figure ABCD is quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9cm and CM = 12 cm. Calculate the area of the quadrilateral.
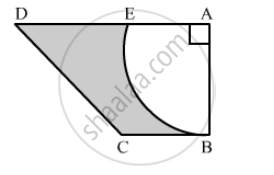
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
The perimeter of a certain sector of a circle of radius 6.5 cm in 31 cm. Find the area of the sector.
On decreasing the radius of a circle by 30%, its area is decreased by
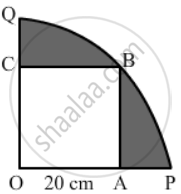
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
The given figures show a rectangle ABCD inscribed in a circle as shown alongside.
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.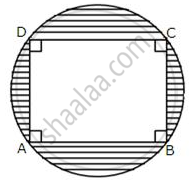
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
The area of the circle is 154 cm2. The radius of the circle is ______.
