Advertisements
Advertisements
प्रश्न
An archery target has three regions formed by three concentric circles as shown in figure. If the diameters of the concentric circles are in the ratios 1 : 2 : 3, then find the ratio of the areas of three regions.
उत्तर

Let the three regions be A, B and C.
The diameters are in the ratio 1 : 2 : 3.
Let the diameters be 1x, 2x and 3x
Then the radius will be `x/2, (2x)/2` and `(3x)/2`
Area of region A = `pi"r"_"A"^2`
= `pi(x/2)^2`
= `pix^2/4`
Area of region B = `pi"r" _"B"^2-pi"r" _"A"^2`
= `pi(x)^2-pi(x/2)^2`
= `(3pi(x)^2)/4`
Area of region C = `pi"r"_"C"^2-pi"r"_"B"^2-pi"r"_"A"^2`
= `pi((3x)/2)^2-pi(x)^2-pi(x/2)^2`
= `pi((3x)/2)^2-(3pix^2)/4`
= `(5pix^2)/4`
Thus, ratio of the areas of regions A, B and C will be
`pix^2/4 : (3pi(x)^2)/4 : (5pix^2)/4`
⇒ 1 : 3 : 5
संबंधित प्रश्न
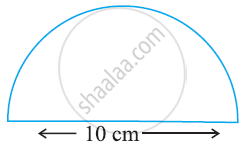
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m . If the length of the rope is increased by 5.5 m , find the increase in area of the grassy lawn in which the calf can graze .
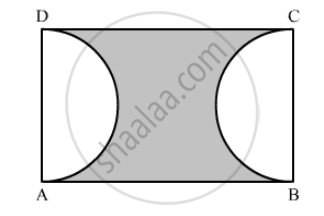
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
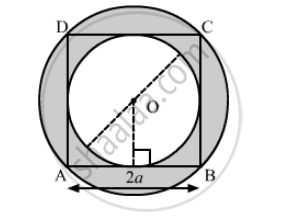
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
The area of incircle of an equilateral triangle is 154 cm2 . The perimeter of the triangle is
The area of a sector whose perimeter is four times its radius r units, is
A circular disc of radius 6 cm is divided into three sectors with central angles 90°,120° and 150°. What part of the whole circle is the sector with central angle 150°? Also, calculate the ratio of the areas of the three sectors.
