Advertisements
Advertisements
प्रश्न
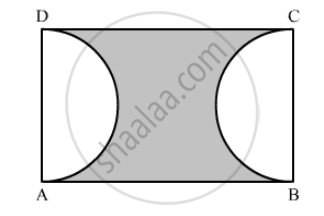
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
उत्तर
Now we will find length of the boundary of the shaded region.
`∴ "Length of the boundary the shaded region"=2pi r+AB+DC`
`∴ "Length of the boundary the shaded region"=2xx22/7xx7+20+20`
`∴ "Length of the boundary the shaded region"=2xx22+40`
`∴ "Length of the boundary the shaded region"=44+40`
`∴ "Length of the boundary the shaded region"=84`
Therefore, length of the boundary of the shaded region is `84 cm`
APPEARS IN
संबंधित प्रश्न
The dimensions of a room are 14 m x 10 m x 6.5 m There are two doors and 4 windows in the room. Each door measures 2.5 m x 1.2 m and each window measures 1.5 m x 1 m. Find the cost of painting the four walls of the room at ₹ `35perm^2` .
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.
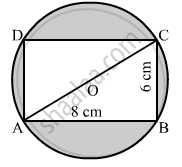
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
The radii of the two circles are 4 cm and 3 cm respectively. The diameter of the circle having an area equal to the sum of the areas of the two circles (in cm) is ____________.
If the radii of two circles are in the ratio of 4 : 3, then their areas are in the ratio of ______.
Find the area of the shaded region: