Advertisements
Advertisements
प्रश्न
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
उत्तर
Let the radius of the circle be r and side of hexagon be a.
Area of hexagon =\[\frac{3\sqrt{3}}{2} a^2\]
\[\Rightarrow 24\sqrt{3} = \frac{3\sqrt{3}}{2} a^2 \]
\[ \Rightarrow a^2 = 16\]
\[ \Rightarrow a = 4 cm\]
In an regular hexagon inscribed in a circle, its side is equal the radius.
∴ r = a = 4 cm
Now, Area of circle is given by
\[\pi r^2 \]
\[ = 3 . 14 \times 4 \times 4\]
\[ = 50 . 24 {cm}^2\]
APPEARS IN
संबंधित प्रश्न
Find the area and perimeter of a square plot of land whose diagonal is 24 m long.
In the following figure, the shaded area is

If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
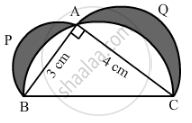
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
The minute hand of a clock is 12 cm long. Find the area swept by in it 35 minutes.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.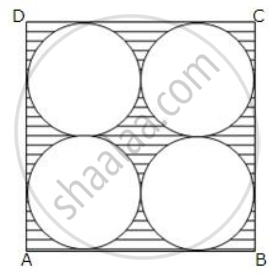
Find the area of the remaining card-board.
Find the area of a ring-shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.
The area of the circle that can be inscribed in a square of side 6 cm is ______.
If the radii of two circles are in the ratio of 4 : 3, then their areas are in the ratio of ______.
