Advertisements
Advertisements
Question
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
Solution
Let the radius of the circle be r and side of hexagon be a.
Area of hexagon =\[\frac{3\sqrt{3}}{2} a^2\]
\[\Rightarrow 24\sqrt{3} = \frac{3\sqrt{3}}{2} a^2 \]
\[ \Rightarrow a^2 = 16\]
\[ \Rightarrow a = 4 cm\]
In an regular hexagon inscribed in a circle, its side is equal the radius.
∴ r = a = 4 cm
Now, Area of circle is given by
\[\pi r^2 \]
\[ = 3 . 14 \times 4 \times 4\]
\[ = 50 . 24 {cm}^2\]
APPEARS IN
RELATED QUESTIONS
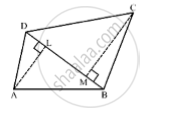
In the given figure ABCD is quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9cm and CM = 12 cm. Calculate the area of the quadrilateral.
Find the area of minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 600 .
If the difference between the circumference and radius of a circle is 37 cm, then using π = \[\frac{22}{7}\] the circumference (in cm) of the circle is
The perimeter of the sector OAB shown in the following figure, is

The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
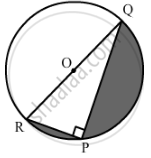
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
The area of a circle is 1386 sq.cm; find its circumference.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

The area of the circular ring enclosed between two concentric circles is 88 cm2. Find the radii of the two circles, if their difference is 1 cm.
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
