Advertisements
Advertisements
Question
If the difference between the circumference and radius of a circle is 37 cm, then using π = \[\frac{22}{7}\] the circumference (in cm) of the circle is
Options
154
44
14
7
Solution
We know that circumference; C of the circle with radius r is equal to`2pir`.
We have given difference between circumference and radius of the circle that is 37 cm.
`∴ C-r=2pir-r`
`∴(2pi-1)r=37`
Substituting `pi=22/7 ` we get,
`∴ (2xx22/7-1)r=37`
`∴ ((44-7)/7)r=37`
`∴(37/7)r=37`
Dividing both sides of the equation by 7/37, we get, `∴r=7`
Therefore, circumference of the circle will be
\[2\pi r = 2 \times \frac{22}{7} \times 7\]
\[ = 44 {cm}^2\]
Hence, the correct choice is (b).
APPEARS IN
RELATED QUESTIONS
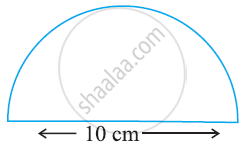
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
The outer circumference of a circular race-track is 528 m . The track is everywhere 14 m wide. Calculate the cost of levelling the track at the rate of 50 paise per square metre.
`(use pi=22/7). `
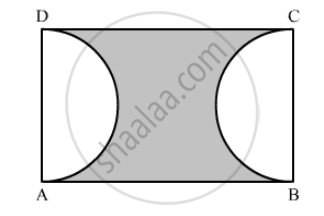
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
If the perimeter of a sector of a circle of radius 6.5 cm is 29 cm, then its area is
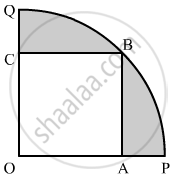
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

On a square cardboard sheet of area 784 cm2, four congruent circular plates of maximum size are placed such that each circular plate touches the other two plates and each side of the square sheet is tangent to two circular plates. Find the area of the square sheet not covered by the circular plates.
