Advertisements
Advertisements
प्रश्न
If the difference between the circumference and radius of a circle is 37 cm, then using π = \[\frac{22}{7}\] the circumference (in cm) of the circle is
पर्याय
154
44
14
7
उत्तर
We know that circumference; C of the circle with radius r is equal to`2pir`.
We have given difference between circumference and radius of the circle that is 37 cm.
`∴ C-r=2pir-r`
`∴(2pi-1)r=37`
Substituting `pi=22/7 ` we get,
`∴ (2xx22/7-1)r=37`
`∴ ((44-7)/7)r=37`
`∴(37/7)r=37`
Dividing both sides of the equation by 7/37, we get, `∴r=7`
Therefore, circumference of the circle will be
\[2\pi r = 2 \times \frac{22}{7} \times 7\]
\[ = 44 {cm}^2\]
Hence, the correct choice is (b).
APPEARS IN
संबंधित प्रश्न
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the lines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the perimeter of the part ABEF.

A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.

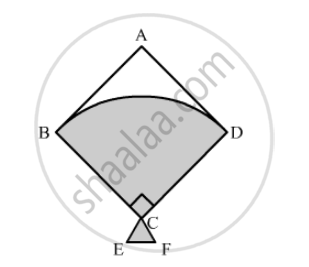
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
Find the area of sector of circle of radius 21 cm and central angle 1200.
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
If a chord of a circle of radius 28 cm makes an angle of 90 ° at the centre, then the area of the major segment is
A rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now graze?
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then ______.
Find the length of the rope by which a bull must be tethered in order that it may be able to graze an area of 2464 m2
Lalitha wants to buy a round carpet of radius is 63 cm for her hall. Find the area that will be covered by the carpet
