Advertisements
Advertisements
Question
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
Solution
Area of the parallelogram = `392 m^2`
Let the base of the parallelogram be b m.
Given:
Height of the parallelogram is twice the base
∴ `Height=2b m`
Area of a parallelogram = Base`xx`Height
⇒ 392=`bxx2b`
⇒`392=2b^2`
⇒`392/2=b^2`
⇒`196=b^2`
⇒ `B=14`
∴ Base=`14 m`
Altitude `2xxBase 2 xx4= 28m`
APPEARS IN
RELATED QUESTIONS
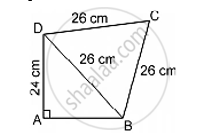
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
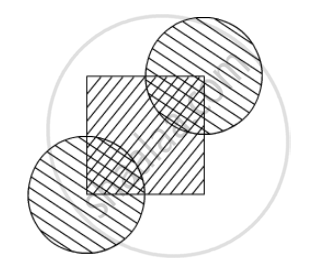
A child makes a poster on a chart paper drawing a square ABCD of side 14 cm. She draws four circles with centre A, B, C and D in which she suggests different ways to save energy. The circles are drawn in such a way that each circle touches externally two of the three remaining circles (in the following figure). In the shaded region she write a message 'Save Energy'. Find the perimeter and area of the shaded region.
(Use π = 22/7)

In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
In the following figure, the area of the segment PAQ is

If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
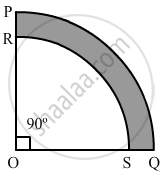
In the given figure, PQRS represents a flower bed. If OP = 21 m and OR = 14 m, find the area of the flower bed.
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
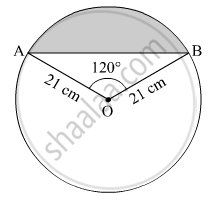
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
The area of the circle is 154 cm2. The radius of the circle is ______.
The area of a circle is 154 cm2. Its diameter is ____________.
