Advertisements
Advertisements
Question
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
Solution
Let r m and R m be the inner and outer boundaries, respectively.
Thus, we have:
2πr = 352
`⇒ r = 352/(2pi)`
Also,
2πR = 396
⇒ 2πR = 396
`⇒ "R" = 396/(2pi)`
Width of the track = (R - r)
`=((396)/(2pi) -(352)/(2pi) )`
`= 1/(2pi)(396-352) "m"`
`=(1/2xx7/22xx44) "m"`
= 7 m
Area of the track =π (R2 - r2)
= [π (R + r) (R - r)
`= [pi(396/(2pi) + (352)/(2pi))xx((396)/(2pi)-(352)/(2pi))]"m"^2`
`=(pixx748/(2pi)xx7)"m"^2`
`=748/2xx7"m"^2`
= 2618 m2
APPEARS IN
RELATED QUESTIONS
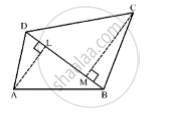
In the given figure ABCD is quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9cm and CM = 12 cm. Calculate the area of the quadrilateral.
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
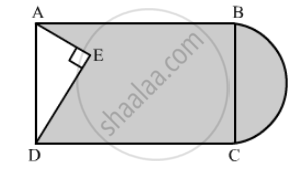
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the lines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the perimeter of the part ABEF.

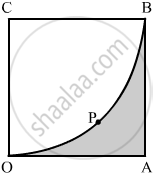
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park.
If AB is a chord of length \[5\sqrt{3}\] cm of a circle with centre O and radius 5 cm, then area of sector OAB is
In the following figure, the area of the shaded region is
The area of a sector whose perimeter is four times its radius r units, is
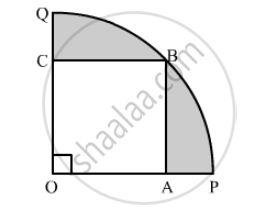
In the given figure, OABC is a square of side 7 cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.