Advertisements
Advertisements
प्रश्न
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
उत्तर
Let r m and R m be the inner and outer boundaries, respectively.
Thus, we have:
2πr = 352
`⇒ r = 352/(2pi)`
Also,
2πR = 396
⇒ 2πR = 396
`⇒ "R" = 396/(2pi)`
Width of the track = (R - r)
`=((396)/(2pi) -(352)/(2pi) )`
`= 1/(2pi)(396-352) "m"`
`=(1/2xx7/22xx44) "m"`
= 7 m
Area of the track =π (R2 - r2)
= [π (R + r) (R - r)
`= [pi(396/(2pi) + (352)/(2pi))xx((396)/(2pi)-(352)/(2pi))]"m"^2`
`=(pixx748/(2pi)xx7)"m"^2`
`=748/2xx7"m"^2`
= 2618 m2
APPEARS IN
संबंधित प्रश्न
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
In a circle of radius 10 cm, an arc subtends an angle of 108° at the centre. what is the area of the sector in terms of π?
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
If diameter of a circle is increased by 40%, then its area increase by
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
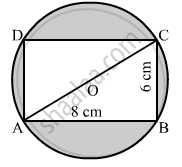
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm2, find the area of the smaller circle.
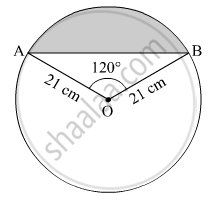
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
