Advertisements
Advertisements
प्रश्न
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
उत्तर
We know that we can cut two circular pieces of equal radii and maximum area from the rectangular cardboard whose diameter is equal to the width of the rectangular cardboard.
∴ Radii of two circuar pieces = Half of the width of the rectangular cardboard = 3.5 cm
Now,
Area of remaining cardboard = Area of rectangular cardboard − 2 ⨯ Area of circular piece having radius 3.5 cm
\[= 14 \times 7 - 2\left( \frac{22}{7} \times 3 . 5 \times 3 . 5 \right)\]
\[ = 98 - 77\]
\[ = 21 {cm}^2\]
Hence, the area of the remaining cardboard is 21 cm2
APPEARS IN
संबंधित प्रश्न
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

The area of sector is one-twelfth that of the complete circle. Find the angle of the sector .
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
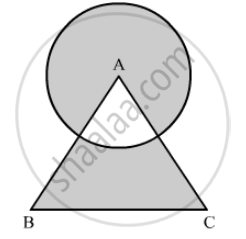
The area of incircle of an equilateral triangle is 154 cm2 . The perimeter of the triangle is
If the area of a circle is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm, then diameter of the large circle (in cm) is
The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
A rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now graze?
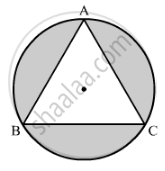
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
Perimeter of a sector of a circle whose central angle is 90° and radius 7 cm is ____________.
The area (in cm2) of the circle that can be inscribed in a square of side 8 cm is ____________.
