Advertisements
Advertisements
Question
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
Solution
We know that we can cut two circular pieces of equal radii and maximum area from the rectangular cardboard whose diameter is equal to the width of the rectangular cardboard.
∴ Radii of two circuar pieces = Half of the width of the rectangular cardboard = 3.5 cm
Now,
Area of remaining cardboard = Area of rectangular cardboard − 2 ⨯ Area of circular piece having radius 3.5 cm
\[= 14 \times 7 - 2\left( \frac{22}{7} \times 3 . 5 \times 3 . 5 \right)\]
\[ = 98 - 77\]
\[ = 21 {cm}^2\]
Hence, the area of the remaining cardboard is 21 cm2
APPEARS IN
RELATED QUESTIONS
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

The perimeter of a rectangular plot of land is 80 m and its breadth is 16 m. Find the length and area of the plot.
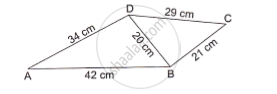
Find the area of the quadrilateral ABCD in which in AB=42 cm, BC=21 cm, CD=29cm, DA=34 cm and diagonal BD = 20 cm.
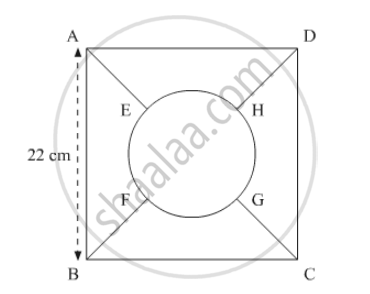
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the ines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the circumference of the central part.
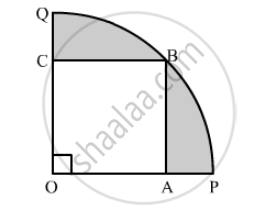
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

The area of incircle of an equilateral triangle is 154 cm2 . The perimeter of the triangle is
ABCD is a rectangle whose three vertices are B (4,0), C (4,3) and D (0, 3). The length of one of its diagonals is
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
Diameter of a circular garden is 9.8 m. Find its area.
