Advertisements
Advertisements
Question
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
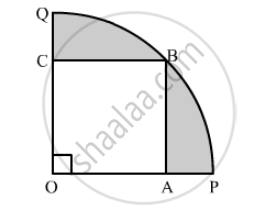
Solution
Construction: Join OB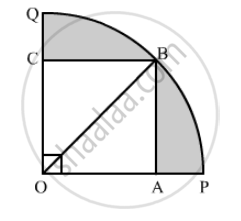
n right triangle AOB
OB2 = OA2 + AB2
= 212 + 212
= 441 + 441
= 882
∴ OB2 = 882
Area of the shaded region = Area of quadrant OPBQ − Area of Square OABC
\[= \frac{1}{4}\pi \left( OB \right)^2 - \left( OA \right)^2 \]
\[ = \frac{1}{4} \times \frac{22}{7} \times 882 - 441\]
\[ = 693 - 441\]
\[ = 252 {cm}^2\]
Hence, the area of the shaded region is 252 cm2.
APPEARS IN
RELATED QUESTIONS
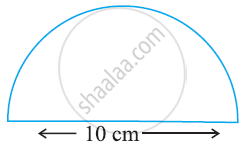
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the lines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the perimeter of the part ABEF.

In the following figure find the area of the shaded region. (Use π = 3.14)
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
An arc subtends an angle of 90° at the centre of the circle of the radius 14 cm. Write the area of minor sector thus formed in terms of π.
If the radius of a circle is diminished by 10%, then its area is diminished by
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
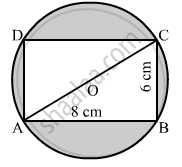
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Write the answer correct to 2 places of decimal.
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
