Advertisements
Advertisements
Question
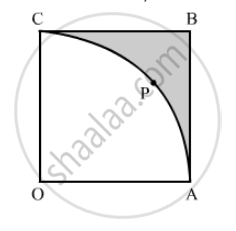
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
Solution
Area of shaded region = Area of square OABC − Area of quadrant OAPC
\[ = \left( 7 \right)^2 - \frac{1}{4} \times \frac{22}{7} \times 7 \times 7\]
\[ = 49 - 38 . 5\]
\[ = 10 . 5 {cm}^2\]
Hence, the area of the shaded region is 10.5 cm2
APPEARS IN
RELATED QUESTIONS
The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
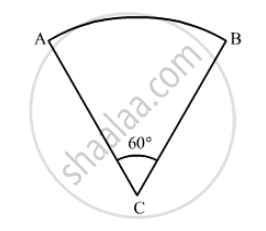
If the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector? (Take \[\pi = 22/7\])
The area of a circle is 220 cm2. The area of ta square inscribed in it is
Find the lengths of the arcs cut off from a circle of radius 12 cm by a chord 12 cm long. Also, find the area of the minor segment.
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
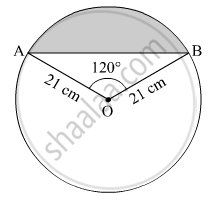
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
Find the area of a flat circular ring formed by two concentric circles (circles with the same centre) whose radii are 9 cm and 5 cm.
Find the area of the biggest circle that can be cut from a rectangular piece 44cm by 28cm. also, find the area of the paper left after cutting out the circle.
If the perimeter of a semicircular protractor is 72 cm where `pi = 22/7`, then the diameter of protractor is ____________.
