Advertisements
Advertisements
Question
What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
Solution
We are given that diameter and side of an equilateral triangle are equal.
Let d and a are the diameter and side of circle and equilateral triangle respectively.
Therefore d = a
We know that area of the circle=`pir^2`
Area of the equilateral triangle =`sqrt3/4 a^2`
Now we will find the ratio of the areas of circle and equilateral triangle.
So, `"Area of circle"/"Area of equilateral triangle"=(pir^2)/(sqrt3/4 a^2)`
We know that radius is half of the diameter of the circle.
⇒` "Area of circle"/"Area of equilateral triangle"=(pi(d/2)^2)/sqrt(3/4 a^2)`
⇒` "Area of circle"/"Area of equilateral triangle"=(pixxd^2/4)/(sqrt3/4 a^2`
Now we will substitute` d=a` in the above equation,
⇒` "Area of circle"/"Area of equilateral triangle"=(pi xx a^2/4)/(sqrt3/4 a^2)`
⇒` "Area of circle"/"Area of equilateral triangle"=pi/sqrt3`
Therefore, ratio of the areas of circle and equilateral triangle is `pi:sqrt3`
APPEARS IN
RELATED QUESTIONS
The area of a square filed is 8 hectares. How long would a man take to cross it diagonally by walking at the rate of 4 km per hour?
The adjacent sides of a parallelogram are 32 cm and 24 cm. If the distance between the longer sides is 17.4 cm, find the distance between the shorter sides.
A calf is tied with a rope of length 6 m at the corner of a square grassy lawn of side 20 m . If the length of the rope is increased by 5.5 m , find the increase in area of the grassy lawn in which the calf can graze .
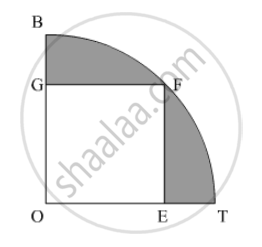
In the following figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
The length of an arc of the sector of angle θ° of a circle with radius R is
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.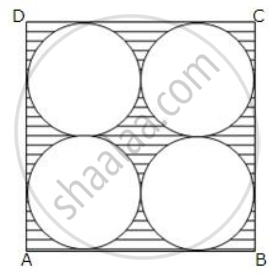
Find the area of the remaining card-board.
The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm2, find the area of the smaller circle.
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
