Advertisements
Advertisements
प्रश्न
What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
उत्तर
We are given that diameter and side of an equilateral triangle are equal.
Let d and a are the diameter and side of circle and equilateral triangle respectively.
Therefore d = a
We know that area of the circle=`pir^2`
Area of the equilateral triangle =`sqrt3/4 a^2`
Now we will find the ratio of the areas of circle and equilateral triangle.
So, `"Area of circle"/"Area of equilateral triangle"=(pir^2)/(sqrt3/4 a^2)`
We know that radius is half of the diameter of the circle.
⇒` "Area of circle"/"Area of equilateral triangle"=(pi(d/2)^2)/sqrt(3/4 a^2)`
⇒` "Area of circle"/"Area of equilateral triangle"=(pixxd^2/4)/(sqrt3/4 a^2`
Now we will substitute` d=a` in the above equation,
⇒` "Area of circle"/"Area of equilateral triangle"=(pi xx a^2/4)/(sqrt3/4 a^2)`
⇒` "Area of circle"/"Area of equilateral triangle"=pi/sqrt3`
Therefore, ratio of the areas of circle and equilateral triangle is `pi:sqrt3`
APPEARS IN
संबंधित प्रश्न
Find the length of the diagonal of a square whose area is `128 cm^2` Also, find its perimeter.
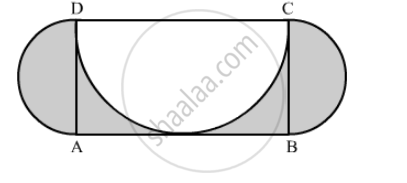
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
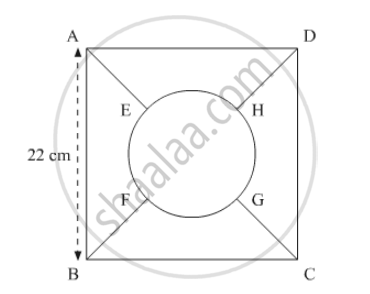
In the following figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the ines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find:
the circumference of the central part.
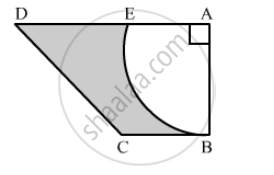
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
If area of a circle inscribed in an equilateral triangle is 48π square units, then perimeter of the triangle is
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

The radii of the two circles are 4 cm and 3 cm respectively. The diameter of the circle having an area equal to the sum of the areas of the two circles (in cm) is ____________.
Area of a rectangle and the area of a circle are equal. If the dimensions of the rectangle are 14 cm × 11 cm, then radius of the circle is ______.
