Advertisements
Advertisements
प्रश्न
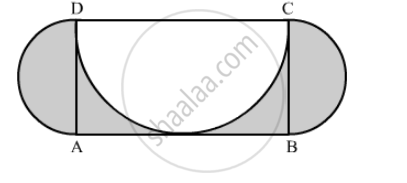
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
उत्तर
Area of the shaded region can be calculated as shown below,
Area of the shaded region = Area of rectangle − area of the semi-circle with diameter DC triangle + 2 `xx`area of two semicircles with diameters AD and BC
`∴ "'Area of the shaded region"=7xx14-(pixx7^2)/2+2xx (pixx3.5^2)/2`
`∴ "Area of the shaded region"=98-pixx49/2+pixx12.25`
Substituting `pi=22/7` we get,
` ∴"Area of the shaded region"=7xx14-pixx7^2/2+2xx pixx3.5`
Substituting `pi=22/7 "We get"`
`∴"Area of the shaded region"=98-(22/7xx49)/2+22/7+12.25`
`∴"Area of the shaded region"=98-(22xx7)/2+22xx1.75`
`∴"Area of the shaded region "98-77+22xx1.75`
`∴"Area of the shaded region "21+38.5`
`∴"Area of the shaded region "=59.5`
Therefore, area of the shaded region is `59.5 cm^2`
APPEARS IN
संबंधित प्रश्न
A footpath of uniform width runs all around the inside of a rectangular field 54m long and 35 m wide. If the area of the path is `420m^2` , find the width of the path.
Find the length of the diagonal of a square whose area is `128 cm^2` Also, find its perimeter.
In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

The perimeter of a triangle is 30 cm and the circumference of its incircle is 88 cm. The area of the triangle is
If the circumference of a circle increases from 4π to 8π, then its area is
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
The circumference of a circular table is 88 m. Find its area.
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be ______.
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.


