Advertisements
Advertisements
प्रश्न
In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

उत्तर
We will first find the length of the boundary.
Length of the boundary = perimeter of semi-circle with diameter AB + boundary of semi-circle with diameter 7 cm
`"Length of the boundary"=(pixx7+pixx3.5)+pixx1.75+pixx1.75`
`"Length of the boundary"=pi(7+3.5+1.75+1.75)`
`"∴Length of the boundary"=14pi`
`"∴Length of the boundary"=44`
Therefore, length of the boundary is44 cm.
Now we will find the area of the shaded region as shown below,
Area of the shaded region = Area of the semi-circle with AB as a diameter − area of the semi-circle with radius AE − area of the semi-circle with radius BC + area of the semi-circle with diameter 7 cm.
`∴ "Area of the shaded region"=(pixx7xx7)/2-(pixx1.75xx1.75)/2-(pixx1.75xx1.75)/2+(pixx3.5xx3.5)/2`
`∴ "Area of the shaded region"=(49pi)/2-3.0625 pi+12.25/2`
`∴ "Area of the shaded region"=(61.25pi)/2-3.0625pi`
`∴ "Area of the shaded region"=(61.25pu-6.125pi)/2`
`∴ "Area of the shaded region" 55.125xx22/7xx1/2`
`∴ "Area of the shaded region"7.87xx11`
`∴ "Area of the shaded region"=86.625`
Therefore, area of the shaded region is ` 86.625 cm^2`
APPEARS IN
संबंधित प्रश्न
A room is 16 m long and 13.5 m broad. Find the cost of covering its floor with 75-m-wide carpet at ₹ 60 per metre.
Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
If he area of a sector of a circle is \[\frac{7}{20}\] of the area of the circle, then the sector angle is equal to
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
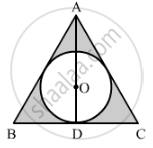
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use `sqrt(3)= 1.73, pi = 3.14]`
A square tank has an area of 1600 cm2. There are four semicircular plots around it. Find the cost of turfing the plots at Rs 12.50 per m2
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centers is 12 cm. Find the diameters of the circle.
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is πb2 cm2? Why?
A table top is semicircular in shape with diameter 2.8 m. Area of this table top is ______.
