Advertisements
Advertisements
प्रश्न
Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
उत्तर
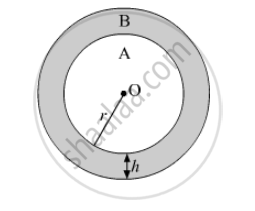
The width of the circular path = h
Let the inner circle be region A and the outer circle be region B
Radius of region A = r
Radius of region B = r + h
Area of the circular path = Area of region B − Area of region A
`= pi(r+h)^2-pir^2`
`= pi(r^2+h^2+2rh-r^2)`
`= pih(h+2r)`
Hence Proved
APPEARS IN
संबंधित प्रश्न
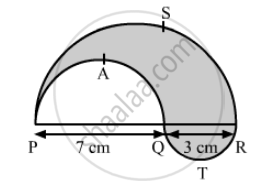
In the the following figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
If the perimeter of a semi-circular protractor is 36 cm, then its diameter is
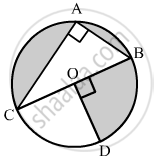
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region.
In the given figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
A sprinkler placed at the centre of a flower garden sprays water covering a circular area. If the area watered is 1386 cm2, find its radius and diameter
The formula used to find the area of the circle is ________ sq.units
The length of the minute hand of a clock is 14 cm. The area swept by the minute hand in 5 minutes is ______.
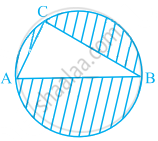
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).