Advertisements
Advertisements
प्रश्न
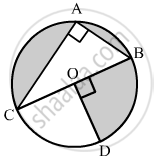
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region.
उत्तर
In right triangle ABC
BC2 = AB2 + AC2
= (7)2 + (24)2
= 49 + 576
= 625
∴ BC2 = 625
⇒ BC = 25
Now, ∠COD + ∠BOD = 180° (Linear pair angles)
⇒∠COD = 180° − 90° = 90°
Now, Area of the shaded region = Area of sector having central angle (360° − 90°) − Area of triangle ABC
`=270^circ/360^circpi(BC)^2 - 1/2"AB" × "AC"`
`= 3/4xx3.14xxx(25/2)^2 - 1/2xx7xx24`
= 367.97 × 84
= 283.97 cm2
Hence, the area of shaded region is 283.97 cm2
APPEARS IN
संबंधित प्रश्न
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
Find the area of the largest triangle that can be inscribed in a semi-circle of radius runits.
The area of the incircle of an equilateral triangle of side 42 cm is
Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made.
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area the circle.
A wire, when bent in the form of a square; encloses an area of 196 cm2. If the same wire is bent to form a circle; find the area of the circle.
Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is πb2 cm2? Why?
How much distance, in metres, a wheel of 25 cm radius will cover if it rotates 350 times?
If the radius of a semi-circular protractor is 7cm, then its perimeter is ______.
